ggplot - Covariation

---

If variation describes the behavior within a variable, covariation describes the behavior between variables. Covariation is the tendency for the values of two or more variables to vary together in a related way.

The best way to spot covariation is to visualize the relationship between two or more variables.

Data

We’ll be using the built-in diamonds and penguins and mpg datasets

Packages

library(tidyverse)
library(palmerpenguins)
library(ggthemes)
library(cowplot)
library(ggridges)

Numerical & Categorical I

---

To visualize the relationship between a numerical and a categorical variable we can use boxplots.

Boxplot

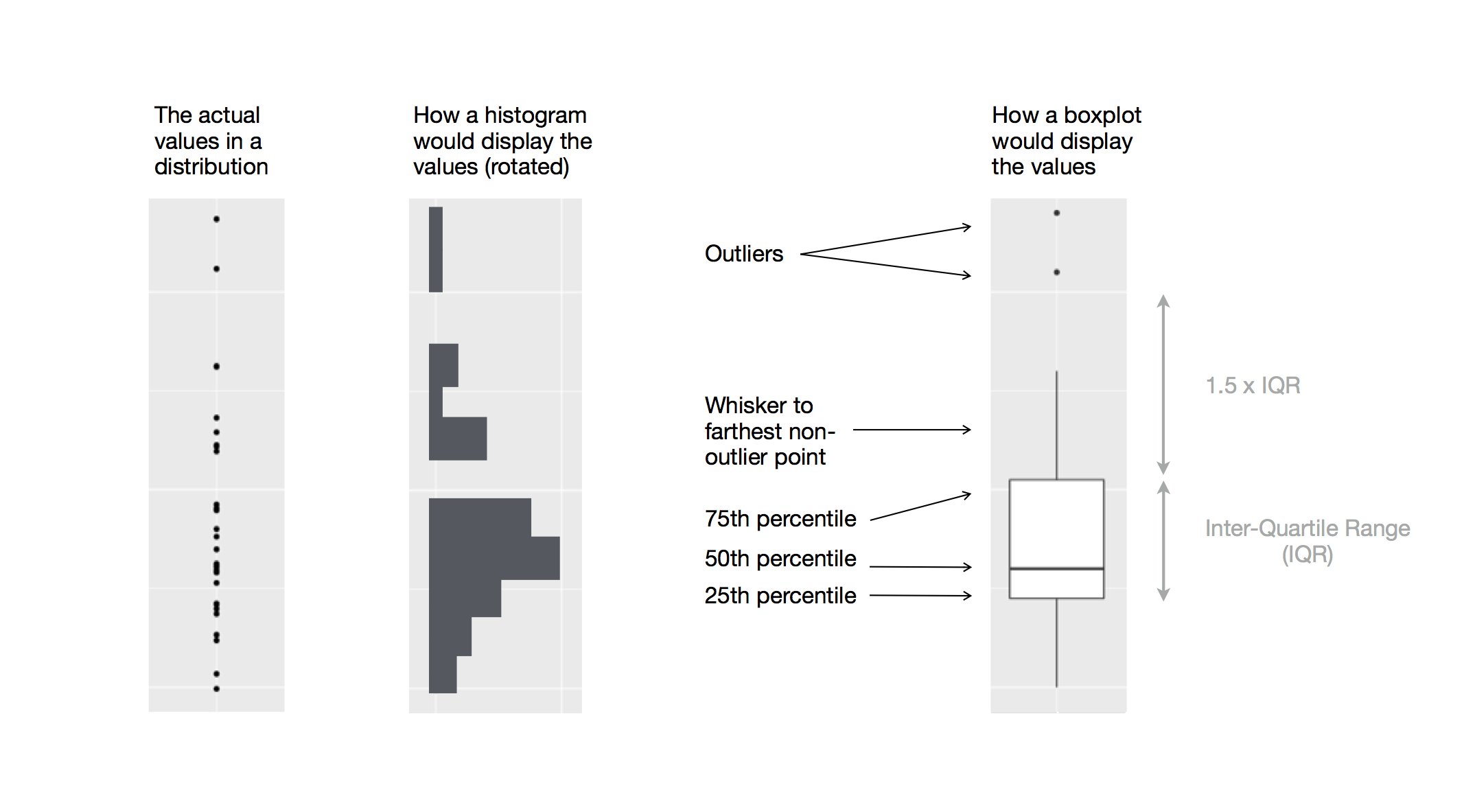
A boxplot is a type of visual shorthand for measures of position (percentiles) that describe a distribution. It is also useful for identifying potential outliers.

Typical values

Are shown in the body of the box or the IQR

Outliers

Each boxplot consists of:

• A box that indicates the range of the middle half of the data, a distance known as the interquartile range (IQR), stretching from the 25th percentile of the distribution to the 75th percentile. In the middle of the box is a line that displays the median, i.e. 50th percentile, of the distribution. These three lines give you a sense of the spread of the distribution and whether or not the distribution is symmetric about the median or skewed to one side.

• Visual points that display observations that fall more than 1.5 times the IQR from either edge of the box. These outlying points are unusual so are plotted individually.

• A line (or whisker) that extends from each end of the box and goes to the farthest non-outlier point in the distribution.

Diagram depicting the definition of a boxplot

Mass per Species

So far we’ve plotted the count for each species with the bar chart, let’s plot the distribution of body mass for each species

ggplot(penguins, aes(x = species, y = body_mass_g)) + 
        geom_boxplot()

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_boxplot()`).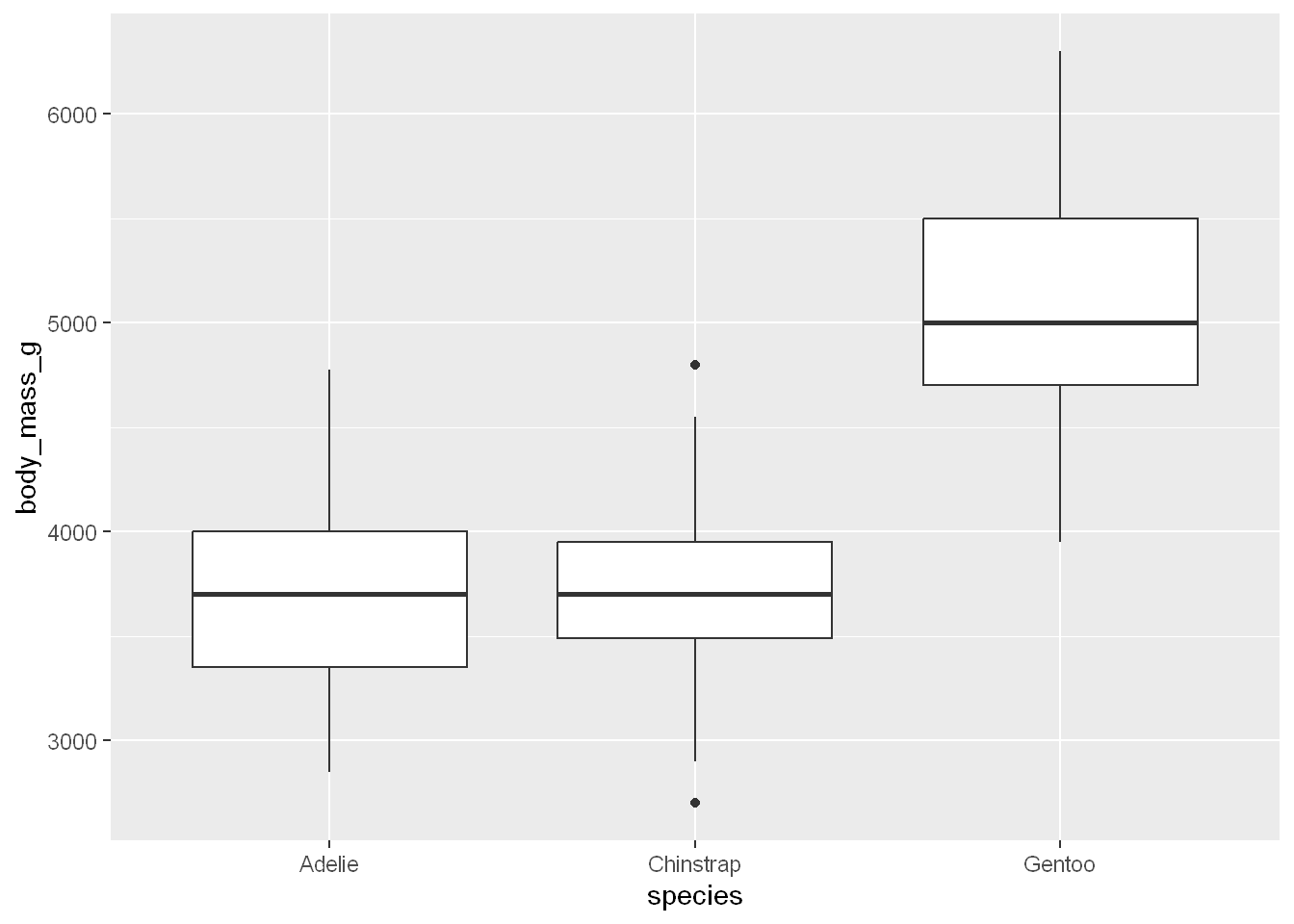

Density of Mass per Species

We’ve plotted the distribution of the density for the body mass variable, and the count for the body mass variable, but now we’re going to plot the density for the body mass variable per species

Linewidth

We’ll customize the line thickness with linewidth

ggplot(penguins, aes(x = body_mass_g, color = species)) +
        geom_density(linewidth = 0.75)

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_density()`).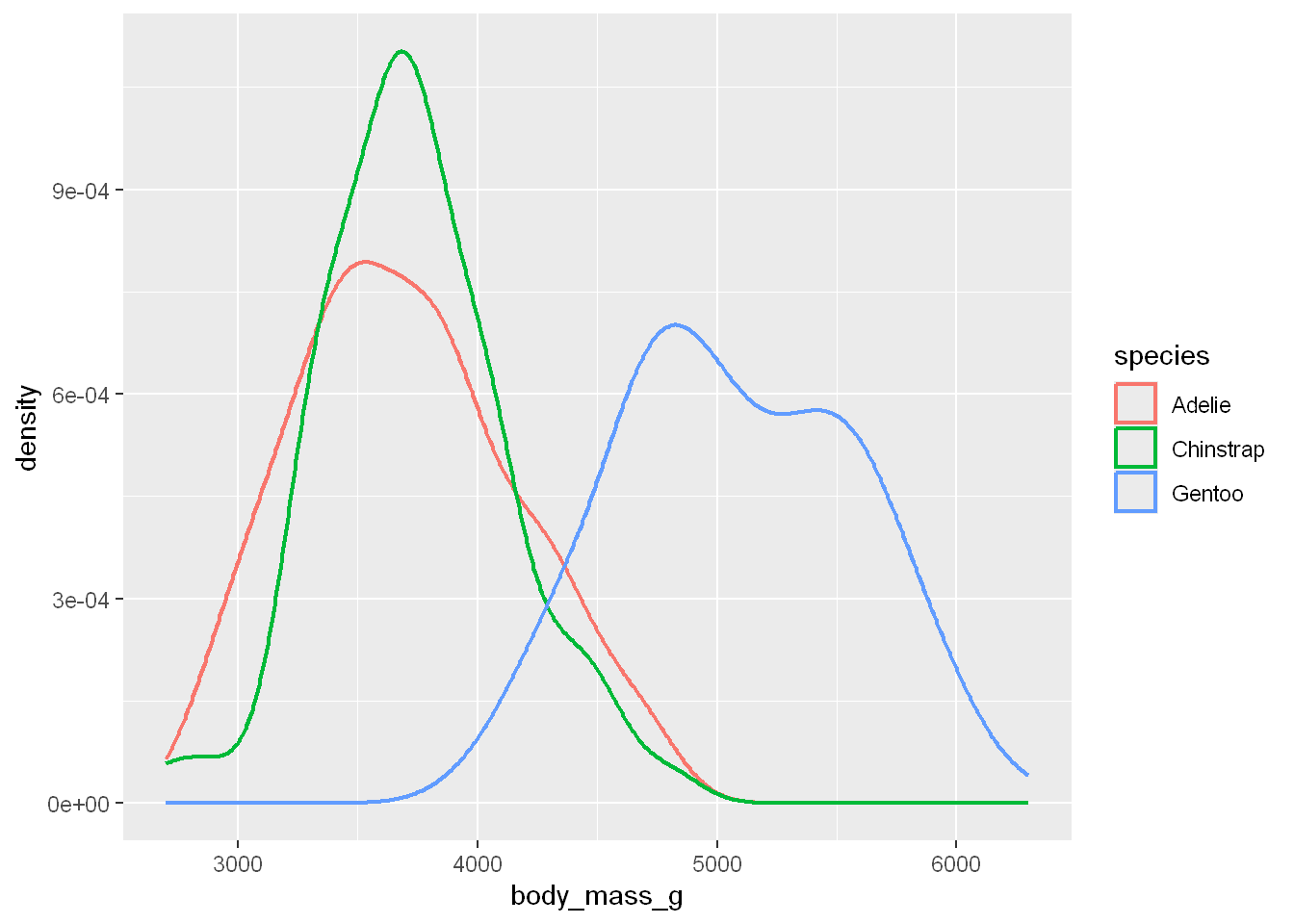

Fill

We’ll fill the areas under the lines with fill instead of using color alone

Alpha

We can add transparency to the fill using alpha

ggplot(penguins, aes(x = body_mass_g, color = species, fill = species)) +
        geom_density(alpha = 0.5)

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_density()`).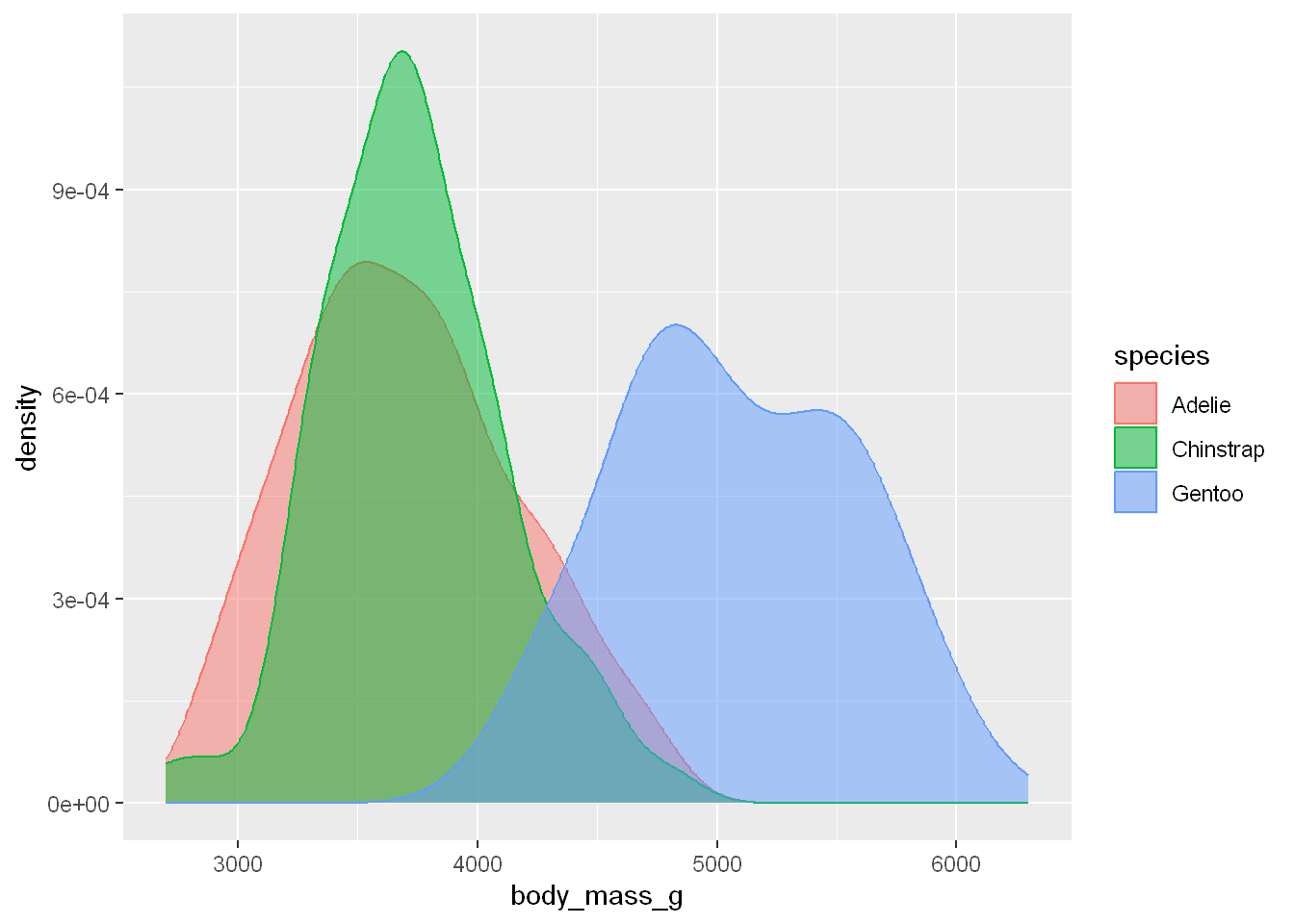

Ridges

The ggridges package (https://wilkelab.org/ggridges) is useful for making ridgeline plots, which can be useful for visualizing the density of a numerical variable for different levels of a categorical variable. 

. In the following plot not only did we use a new geom (geom_density_ridges()), but we have also mapped the same variable to multiple aesthetics (drv to y, fill, and color) as well as set an aesthetic (alpha = 0.5) to make the density curves transparent.

ggplot(mpg, aes(x = hwy, y = drv, fill = drv, color = drv)) + 
        geom_density_ridges(alpha = 0.5, show.legend = FALSE)

Picking joint bandwidth of 1.28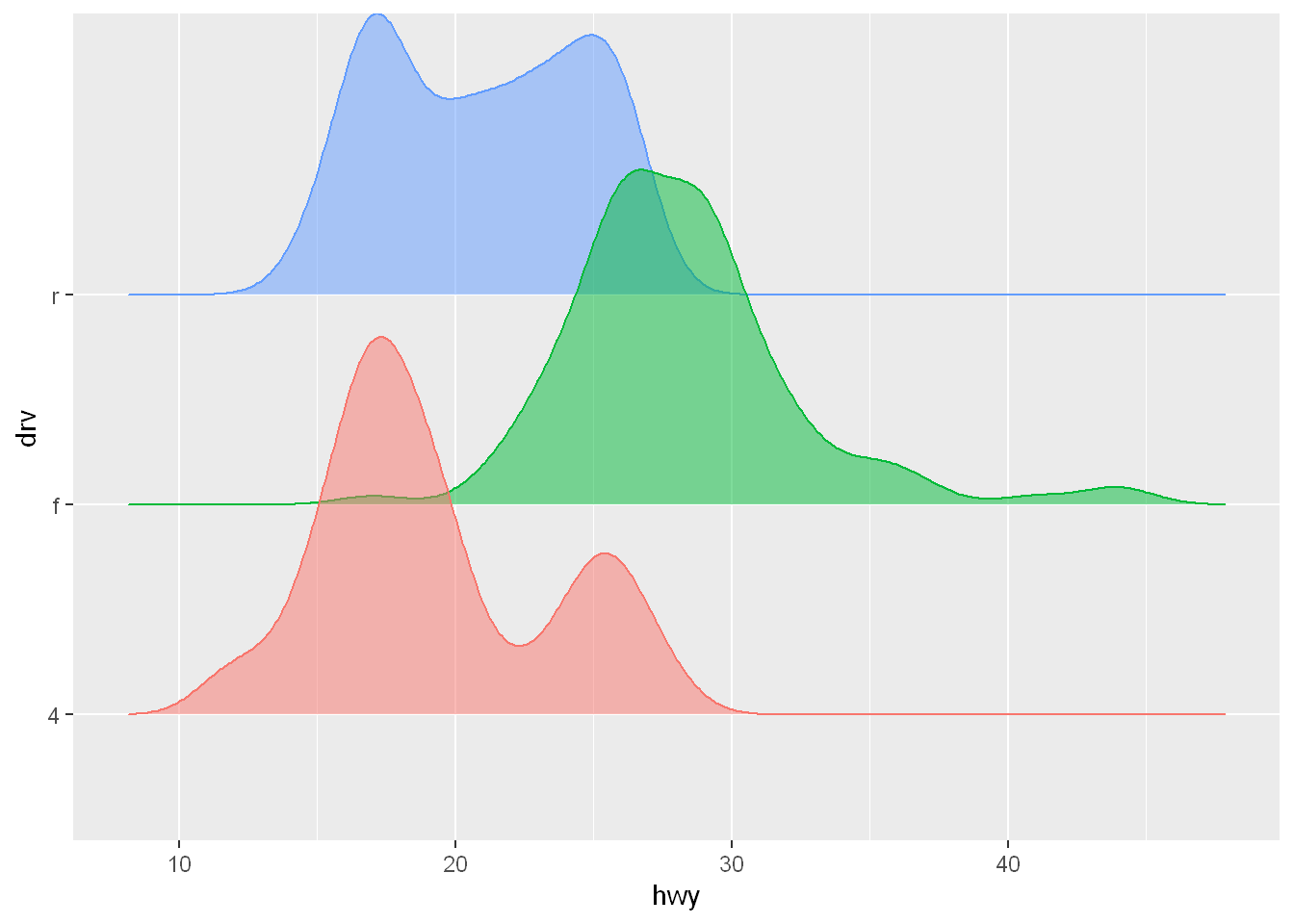

#> Picking joint bandwidth of 1.28

Viz

Sometimes it’s best to combine all three plots together, histogram, density and boxplot to convey the point clearly. Next I’ll show you how to completely change the look of your presentation by using a different geom with the same data.

1. Histogram shows the distribution and count of the highway mpg data

2. Density line shows the outline of the frequency of the highway mpg data

3. Boxplot shows the 50% of the data concentration along with the range and outliers

q1 <- ggplot(mpg, aes(x = hwy)) +   geom_histogram(binwidth = 2) 
q2 <- ggplot(mpg, aes(x = hwy)) +   geom_density() 
q3 <- ggplot(mpg, aes(x = hwy)) +   geom_boxplot() 
plot_grid(q1, q2, q3)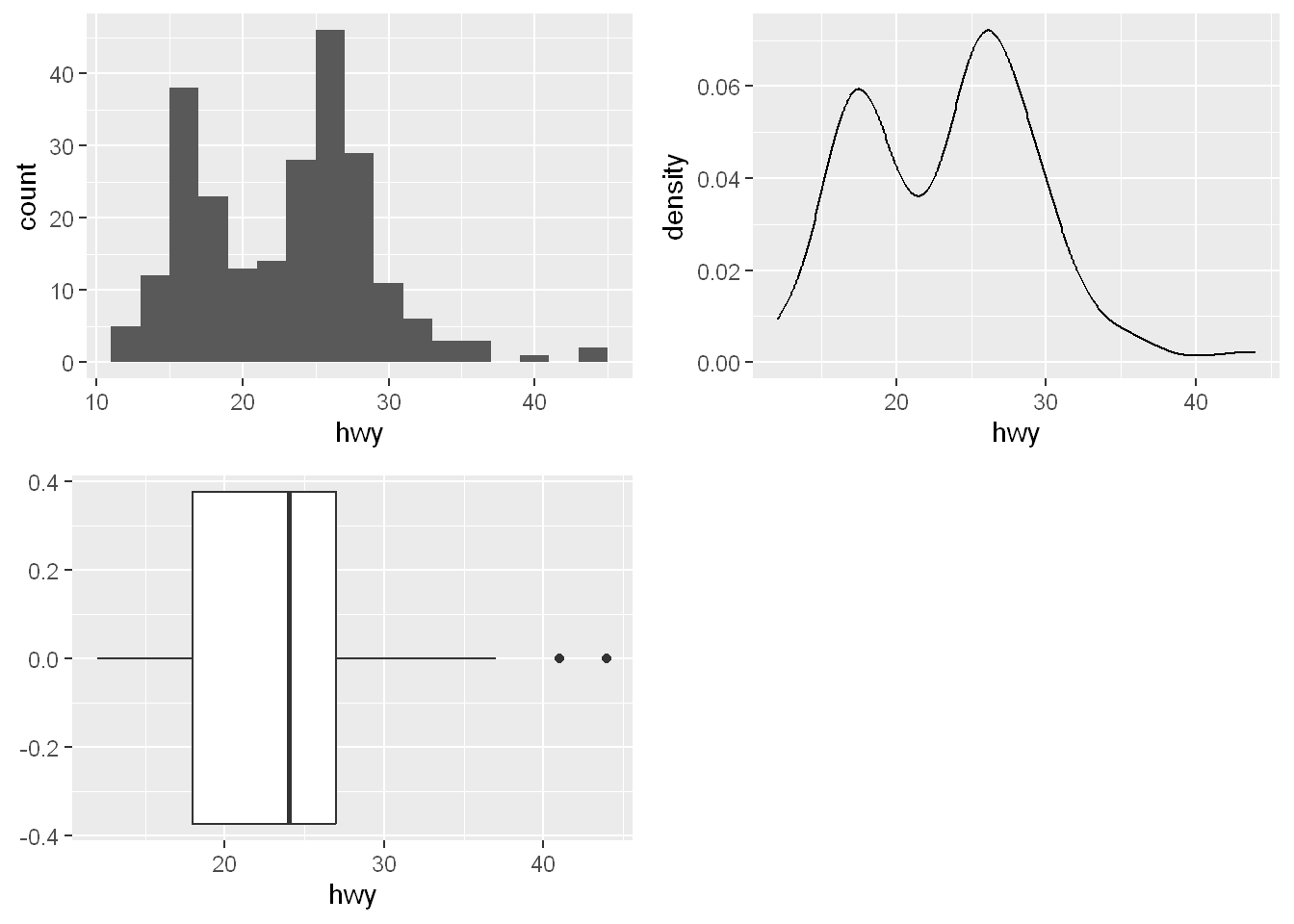

Numerical & Categorical II

---

For example, let’s explore how the price of a diamond varies with its quality (measured by cut) using geom_freqpoly():

ggplot(diamonds, aes(x = price)) + 
  geom_freqpoly(aes(color = cut), binwidth = 500, linewidth = 0.75)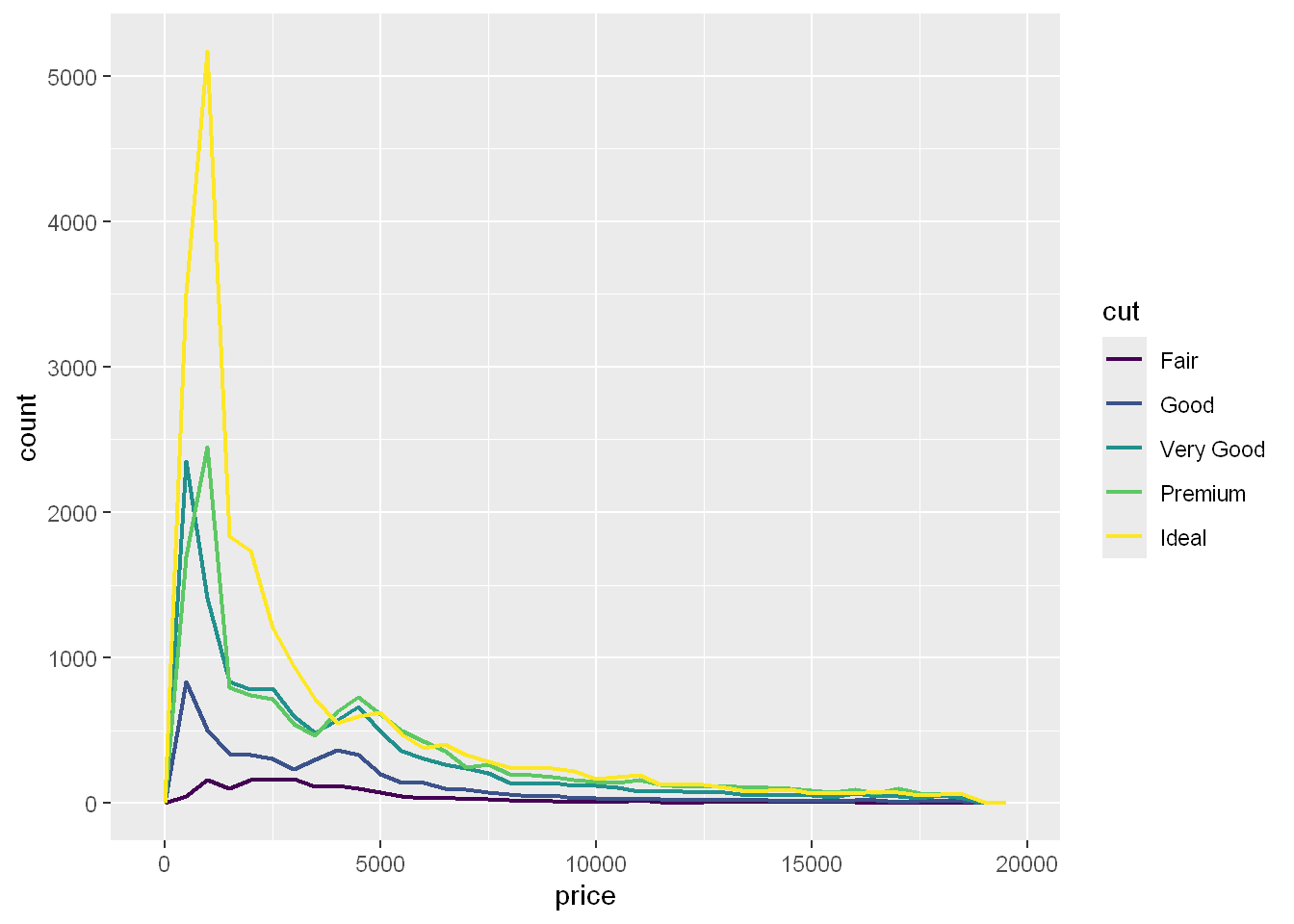

Note that ggplot2 uses an ordered color scale for cut because it’s defined as an ordered factor variable in the data. You’ll learn more about these in ?@sec-ordered-factors.

The default appearance of geom_freqpoly() is not that useful here because the height, determined by the overall count, differs so much across cuts, making it hard to see the differences in the shapes of their distributions.

Density

To make the comparison easier we need to swap what is displayed on the y-axis. Instead of displaying count, we’ll display the

density, which is the count standardized so that the area under each frequency polygon is one.

Note that we’re mapping the density to y, but since density is not a variable in the diamonds dataset, we need to first calculate it. We use the after_stat() function to do so.

After_stat

In order to map from stat transformed data you should use the after_stat() function to flag that

evaluation of the aesthetic mapping should be postponed until after stat transformation. Evaluation after stat transformation will have access to the variables calculated by the stat, not the original mapped values.

The ‘computed variables’ section in each stat lists which variables are available to access.

ggplot(diamonds, aes(x = price, y = after_stat(density))) + 
  geom_freqpoly(aes(color = cut), binwidth = 500, linewidth = 0.75)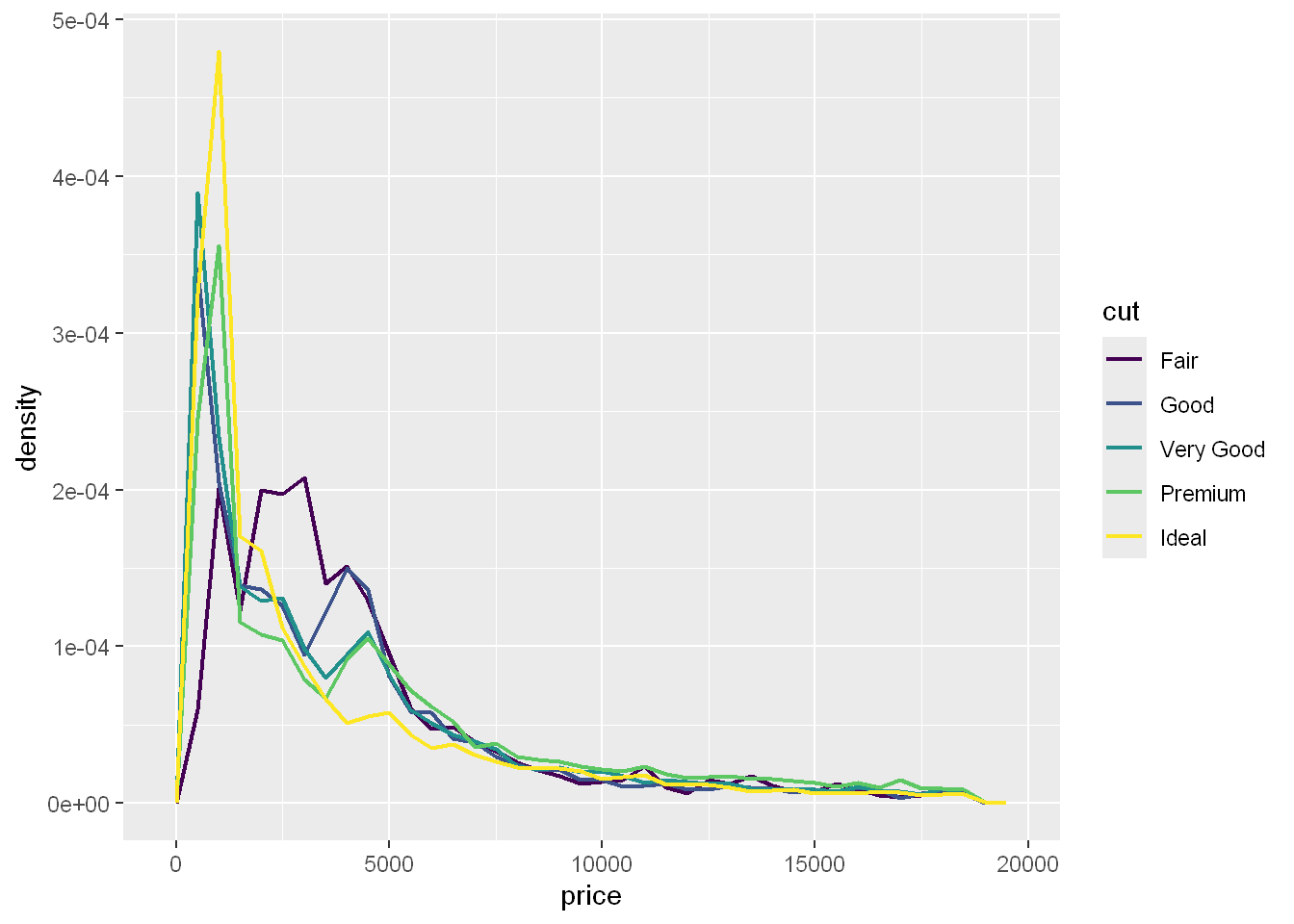

There’s something rather surprising about this plot - it appears that fair diamonds (the lowest quality) have the highest average price! But maybe that’s because frequency polygons are a little hard to interpret.

Boxplot

A visually simpler plot for exploring this relationship is using side-by-side boxplots.

ggplot(diamonds, aes(x = cut, y = price)) +
  geom_boxplot()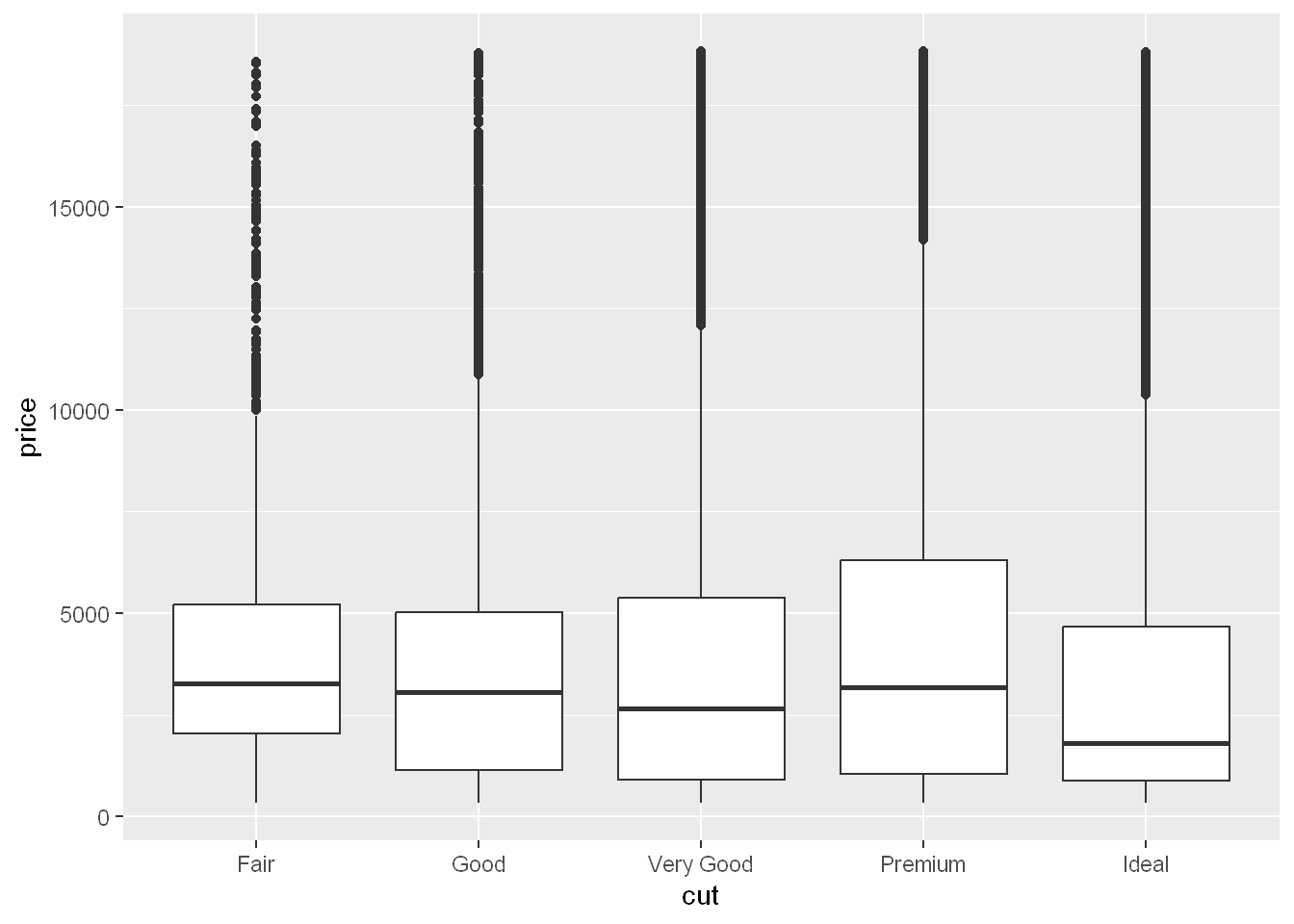

We see much less information about the distribution, but the boxplots are much more compact so we can more easily compare them (and fit more on one plot). It supports the counter-intuitive finding that better quality diamonds are typically cheaper!

Ordered factor

cut is an ordered factor: fair is worse than good, which is worse than very good and so on. Many categorical variables don’t have such an intrinsic order, so you might want to reorder them to make a more informative display.

Fct_reorder

One way to do that is with fct_reorder(). You’ll learn more about that function in ?@sec-modifying-factor-order, but we want to give you a quick preview here because it’s so useful. For example, take the class variable in the mpg dataset. You might be interested to know how highway mileage varies across classes:

ggplot(mpg, aes(x = class, y = hwy)) +
  geom_boxplot()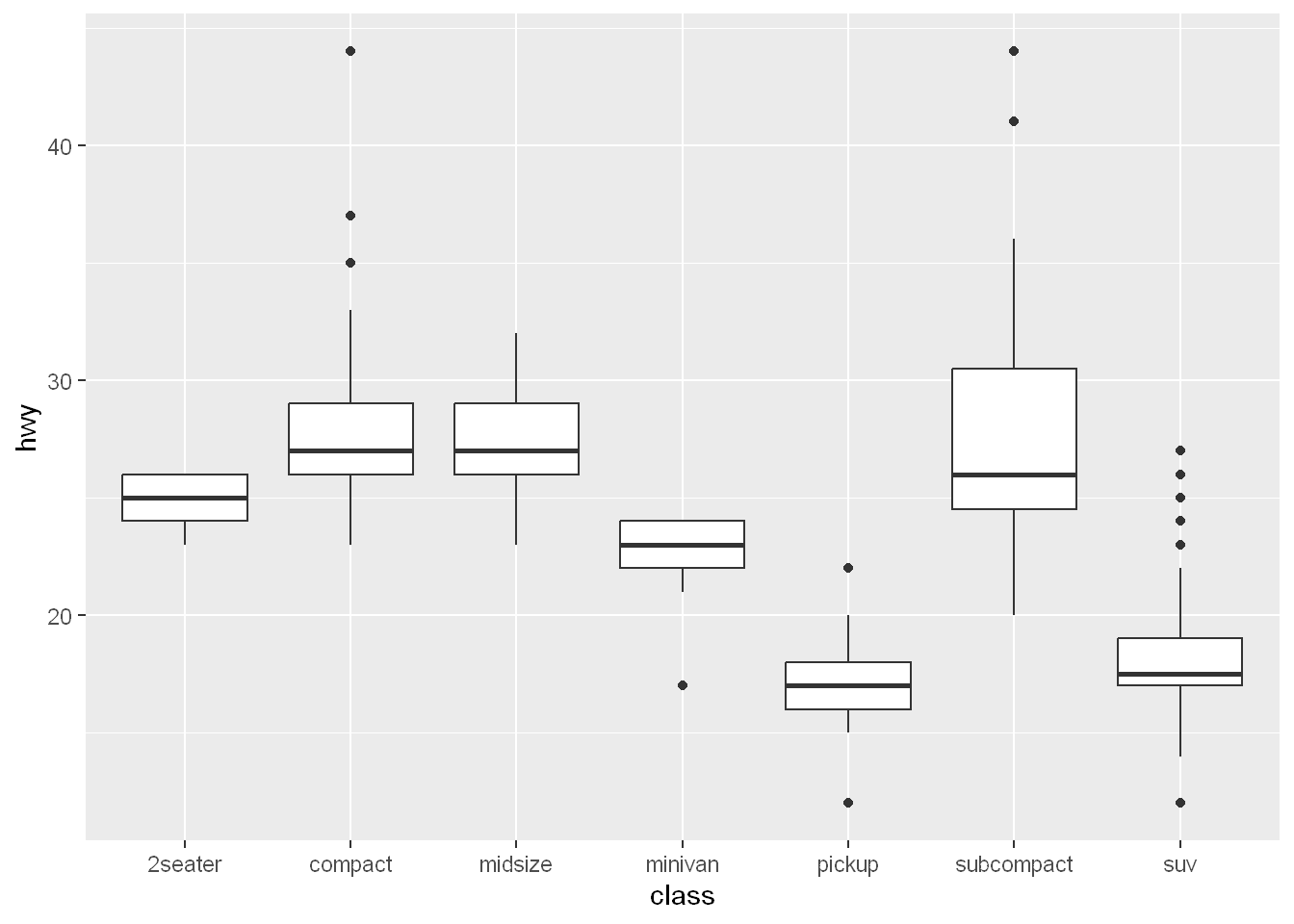

To make the trend easier to see, we can reorder class based on the median value of hwy:

ggplot(mpg, aes(x = fct_reorder(class, hwy, median), y = hwy)) +
  geom_boxplot()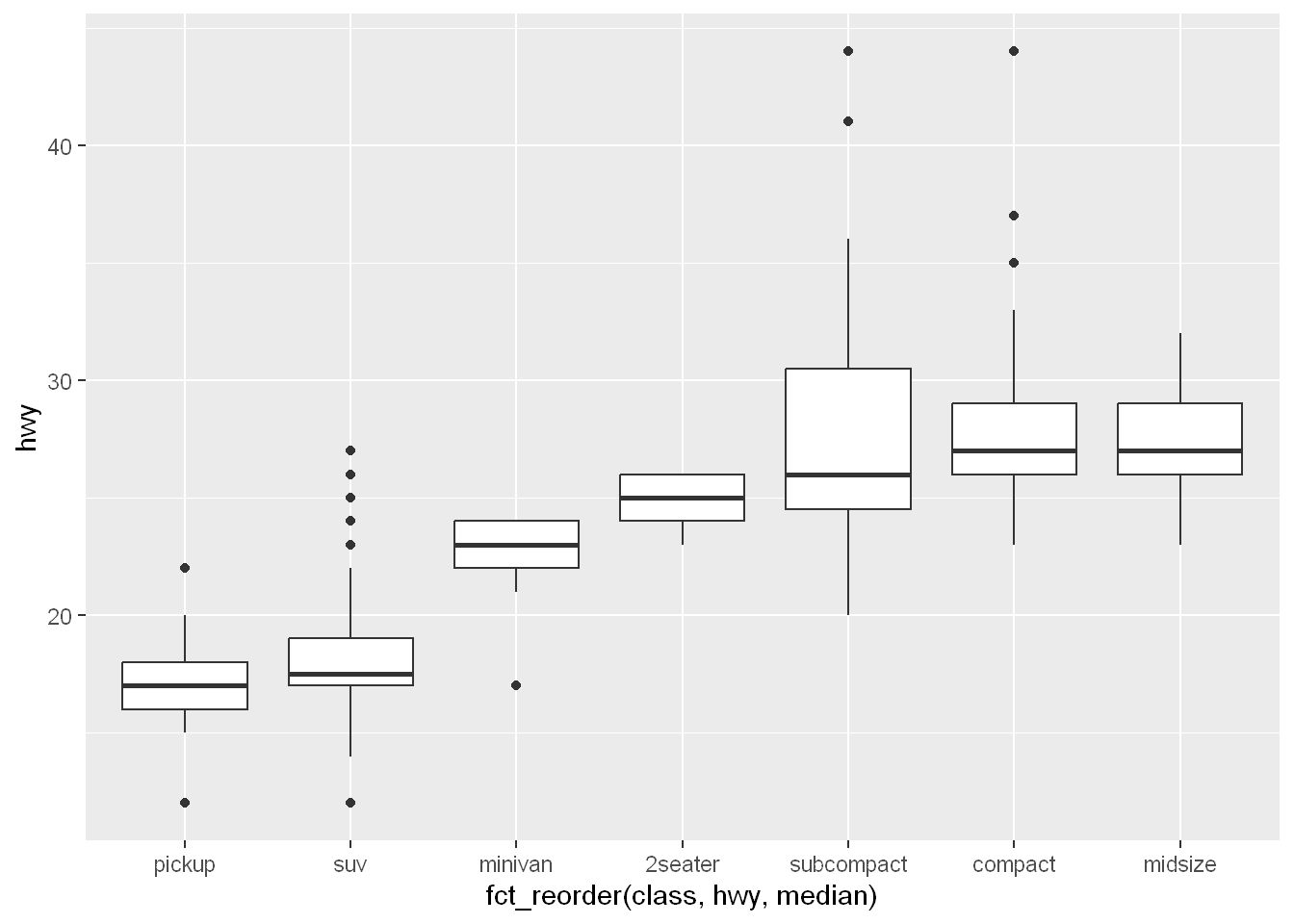

Flip Plot

---

If you have long variable names, geom_boxplot() will work better if you flip it 90°. You can do that by exchanging the x and y aesthetic mappings.

ggplot(mpg, aes(x = hwy, y = fct_reorder(class, hwy, median))) +
  geom_boxplot()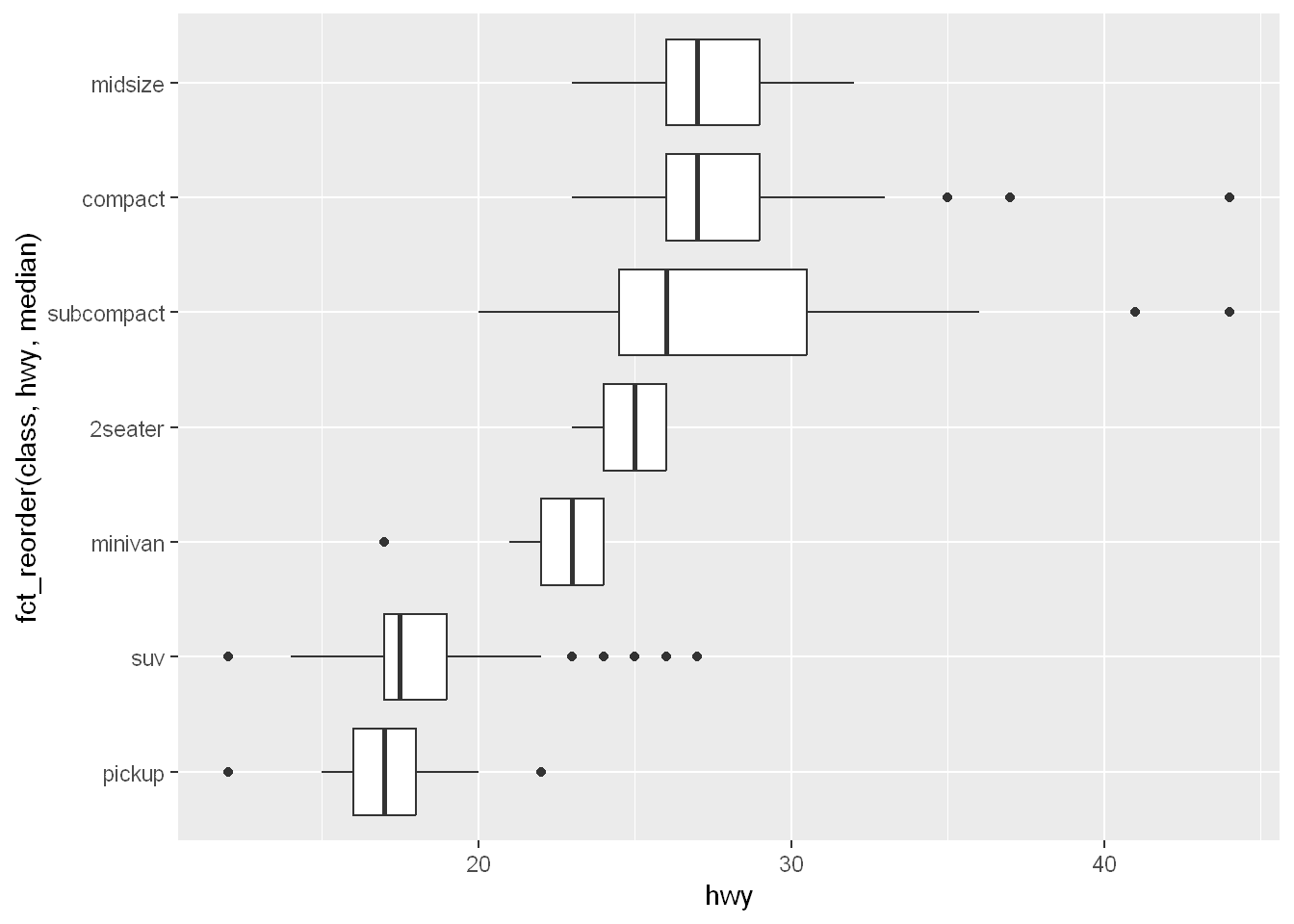

Observations

1. Use what you’ve learned to improve the visualization of the departure times of cancelled vs. non-cancelled flights.
2. Based on EDA, what variable in the diamonds dataset appears to be most important for predicting the price of a diamond? How is that variable correlated with cut? Why does the combination of those two relationships lead to lower quality diamonds being more expensive?
3. Instead of exchanging the x and y variables, add coord_flip() as a new layer to the vertical boxplot to create a horizontal one. How does this compare to exchanging the variables?
4. One problem with boxplots is that they were developed in an era of much smaller datasets and tend to display a prohibitively large number of “outlying values”. One approach to remedy this problem is the letter value plot. Install the lvplot package, and try using geom_lv() to display the distribution of price vs. cut. What do you learn? How do you interpret the plots?
5. Create a visualization of diamond prices vs. a categorical variable from the diamonds dataset using geom_violin(), then a faceted geom_histogram(), then a colored geom_freqpoly(), and then a colored geom_density(). Compare and contrast the four plots. What are the pros and cons of each method of visualizing the distribution of a numerical variable based on the levels of a categorical variable?
6. If you have a small dataset, it’s sometimes useful to use geom_jitter() to avoid overplotting to more easily see the relationship between a continuous and categorical variable. The ggbeeswarm package provides a number of methods similar to geom_jitter(). List them and briefly describe what each one does.

Two Categorical Vars

---

Stacked Bar chart

We can use stacked bar plots to visualize the relationship between two categorical variables. For example, the following two stacked bar plots both display the relationship between island and species, or specifically, visualizing the distribution of species within each island.

ggplot(penguins, aes(x = island, fill = species)) + 
        geom_bar()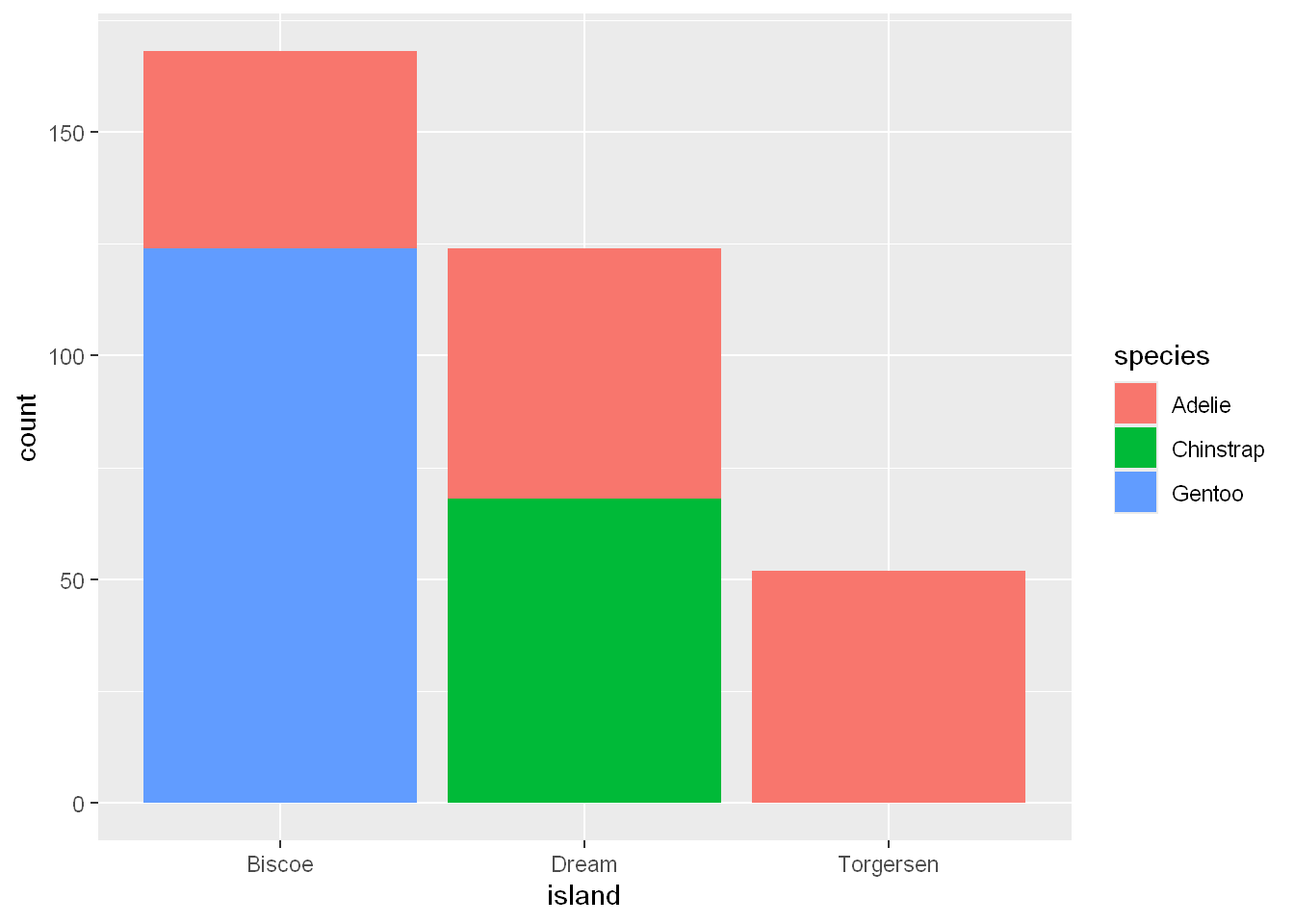

If you observe the numbers of Adelies on each island, it appears to be equal, but hard to tell from the chart, as this shows the frequencies of each species of penguins on each island.

What if we plot a chart where the bar are sized in relation to each other?

Fill Stacked Bars

position = fill

In other words, out of all the penguins on each island, which species present what percentage of the entire island population of penguins? This second one is arelative frequency plot created by setting position = "fill" in the geom, is more useful for comparing species distributions across islands since it’s not affected by the unequal numbers of penguins across the islands.

1. Using this plot we can see that Gentoo penguins all live on Biscoe island and make up roughly 75% of the penguins on that island

2. Chinstrap all live on Dream island and make up roughly 50% of the penguins on that island

3. Adelie live on all three islands and make up all of the penguins on Torgersen.

ggplot(penguins, aes(x = island, fill = species)) + 
        geom_bar(position = "fill")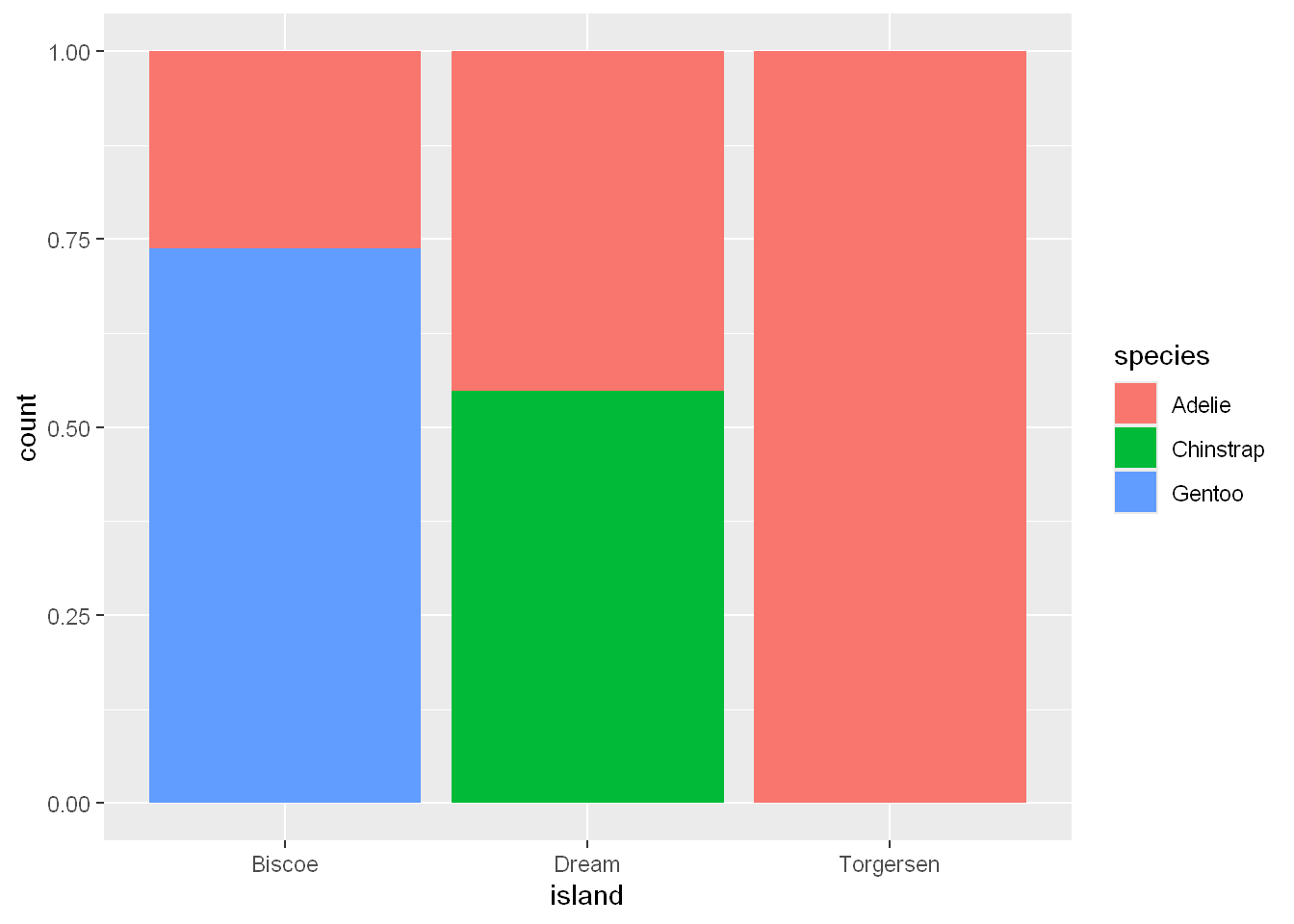

geom_count

To visualize the covariation between categorical variables, you’ll need to count the number of observations for each combination of levels of these categorical variables. One way to do that is to rely on the built-in geom_count():

ggplot(diamonds, aes(x = cut, y = color)) +
        geom_count()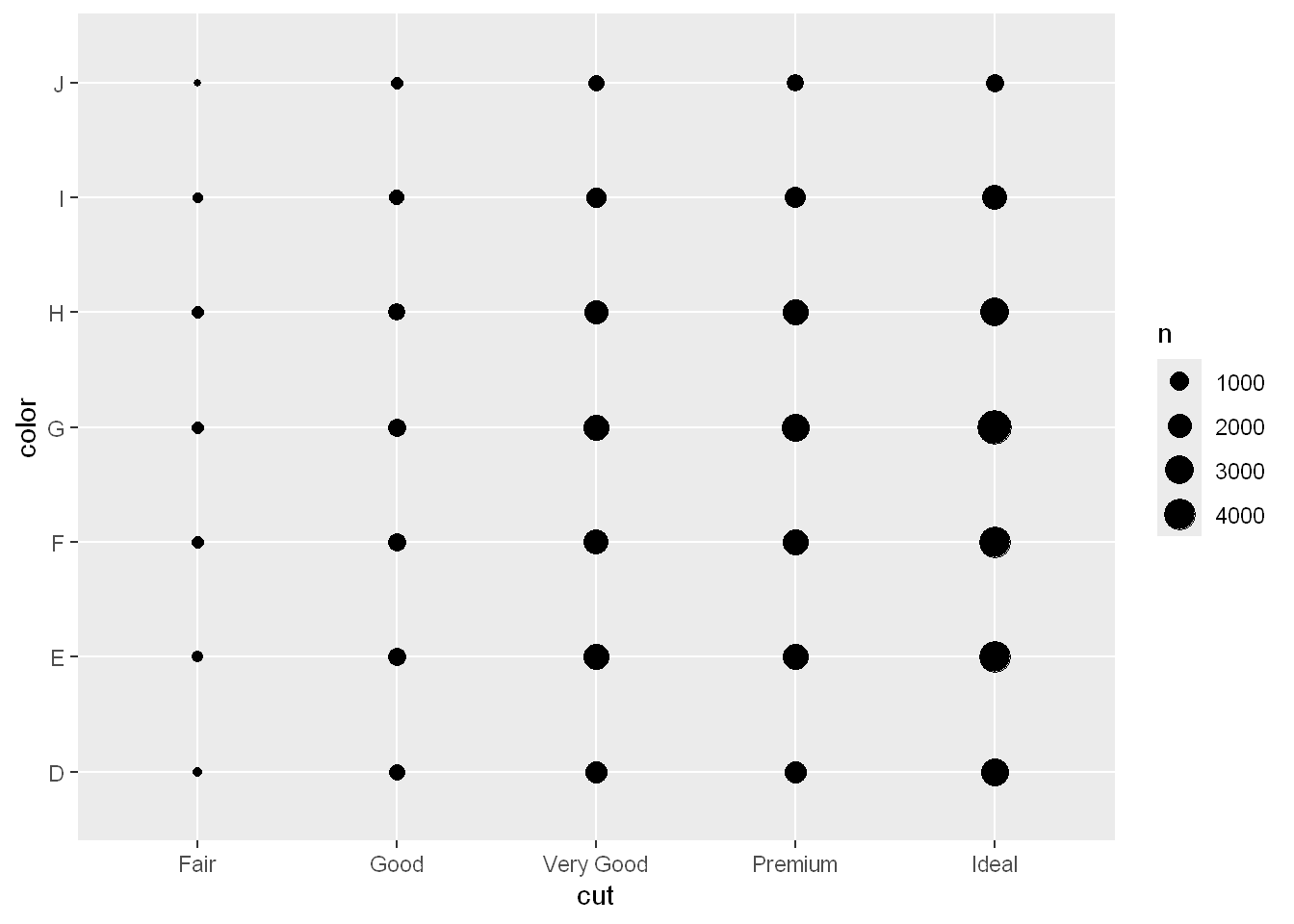

The size of each circle in the plot displays how many observations occurred at each combination of values. Covariation will appear as a strong correlation between specific x values and specific y values.

Count

Another approach for exploring the relationship between these variables is computing the counts with dplyr:

diamonds |>
        count(color, cut)

# A tibble: 35 × 3
   color cut           n
   <ord> <ord>     <int>
 1 D     Fair        163
 2 D     Good        662
 3 D     Very Good  1513
 4 D     Premium    1603
 5 D     Ideal      2834
 6 E     Fair        224
 7 E     Good        933
 8 E     Very Good  2400
 9 E     Premium    2337
10 E     Ideal      3903
# ℹ 25 more rows

HeatMap

---

geom_tile

Then visualize with geom_tile() and the fill aesthetic:

 diamonds |>  count(color, cut) |>  ggplot(aes(x = color, y = cut)) + 
        geom_tile(aes(fill = n))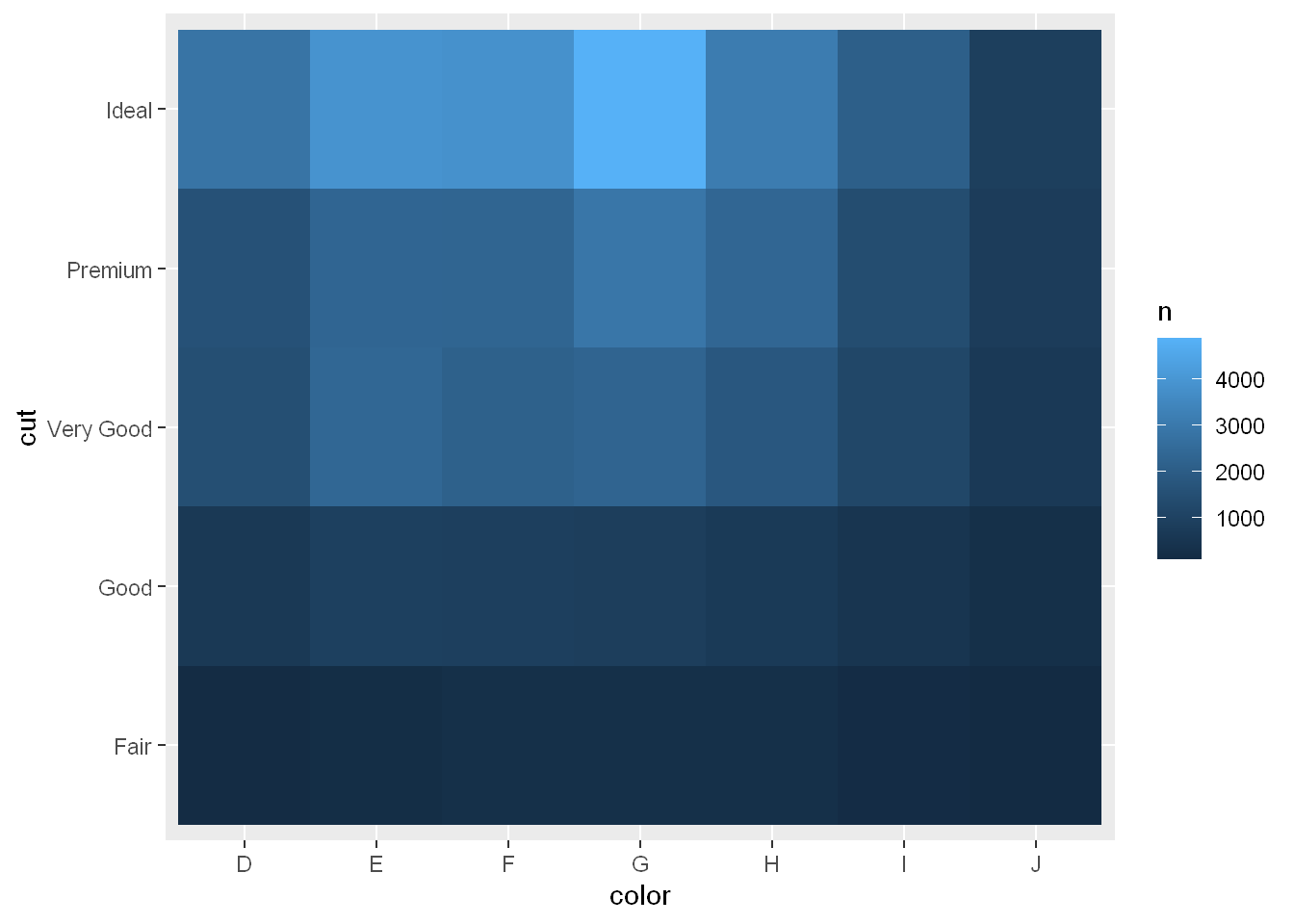

If the categorical variables are unordered, you might want to use the seriation package to simultaneously reorder the rows and columns in order to more clearly reveal interesting patterns. For larger plots, you might want to try the heatmaply package, which creates interactive plots.

Observations

1. How could you rescale the count dataset above to more clearly show the distribution of cut within color, or color within cut?
2. What different data insights do you get with a segmented bar chart if color is mapped to the x aesthetic and cut is mapped to the fill aesthetic? Calculate the counts that fall into each of the segments.
3. Use geom_tile() together with dplyr to explore how average flight departure delays vary by destination and month of year. What makes the plot difficult to read? How could you improve it?

Two Numerical Values

---

Scatterplot

We’ve covered how scatterplots created with geom_point() and geom_smooth() are for visualizing the relationship between two numerical variables.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) + 
        geom_point()

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).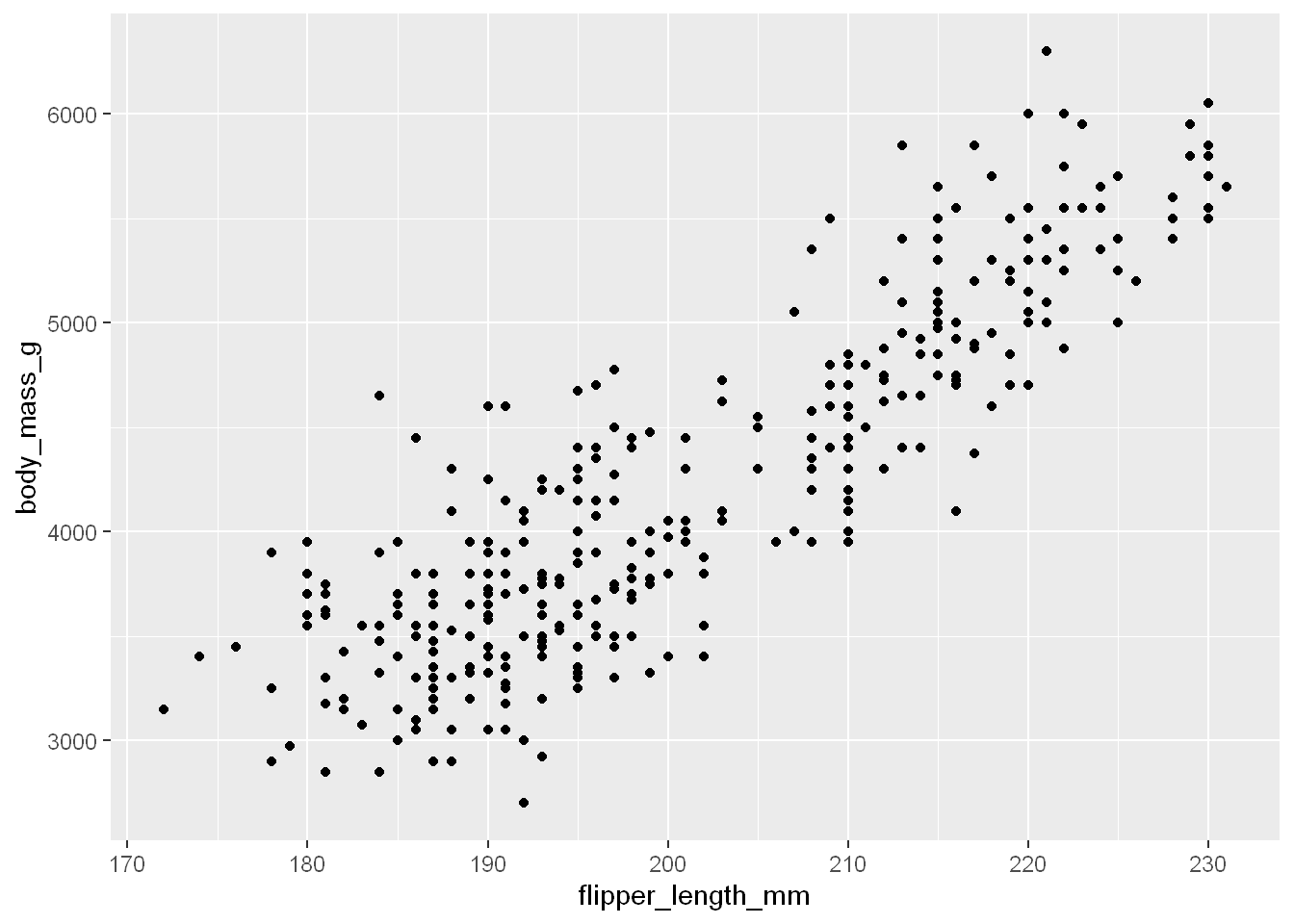

geom_point

First let’s filter the dataset to smaller of the columns we need:

smaller <- diamonds |>
        filter(carat < 3)

You’ve already seen one great way to visualize the covariation between two numerical variables: draw a scatterplot with geom_point(). You can see covariation as a pattern in the points. For example, you can see a positive relationship between the carat size and price of a diamond: diamonds with more carats have a higher price. The relationship is exponential.

(In this section we’ll use the smaller dataset to stay focused on the bulk of the diamonds that are smaller than 3 carats)

 ggplot(smaller, aes(x = carat, y = price)) + 
        geom_point()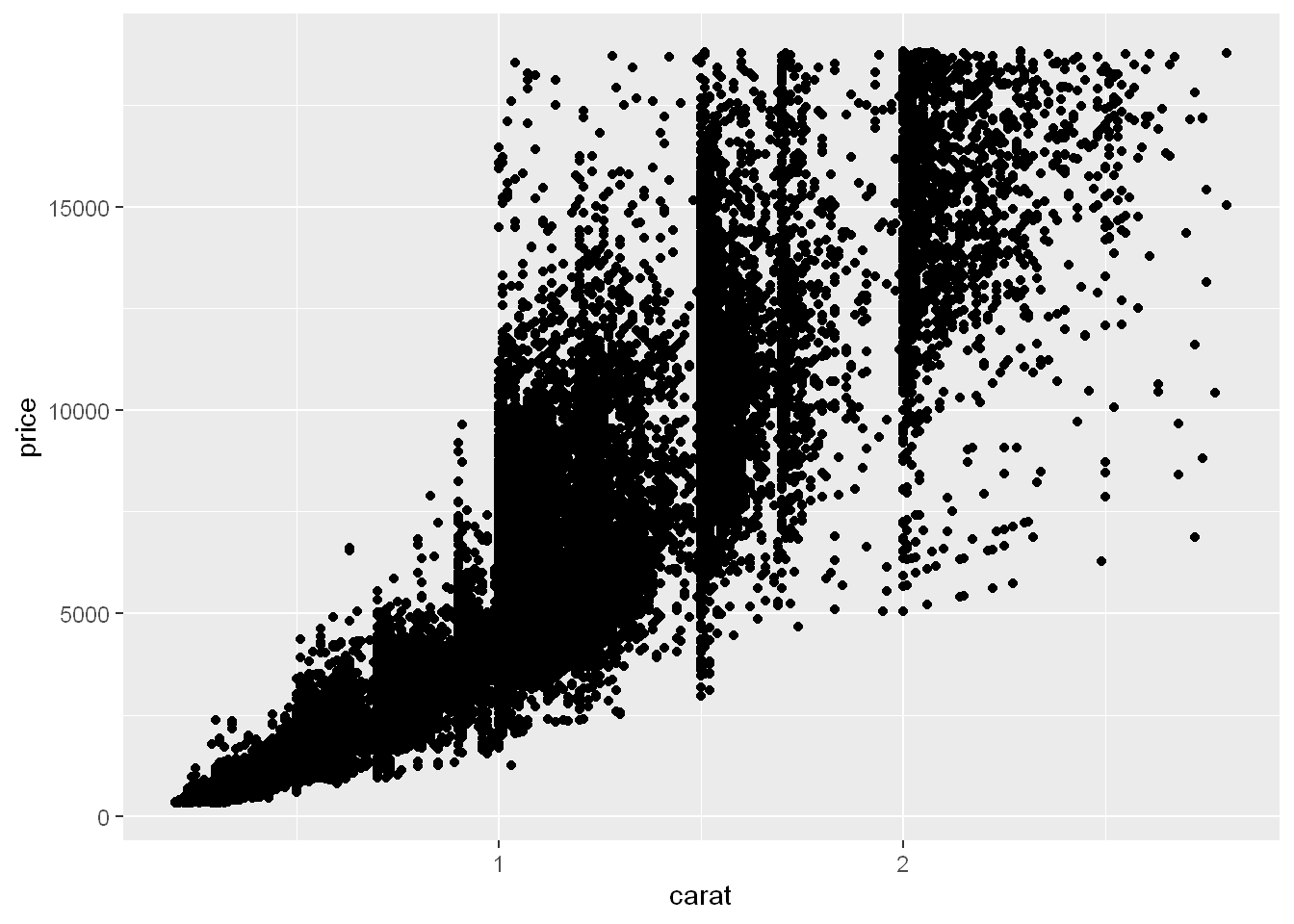

alpha

Scatterplots become less useful as the size of your dataset grows, because points begin to overplot, and pile up into areas of uniform black, making it hard to judge differences in the density of the data across the 2-dimensional space as well as making it hard to spot the trend. You’ve already seen one way to fix the problem: using the alpha aesthetic to add transparency.

ggplot(smaller, aes(x = carat, y = price)) +
        geom_point(alpha = 1 / 100)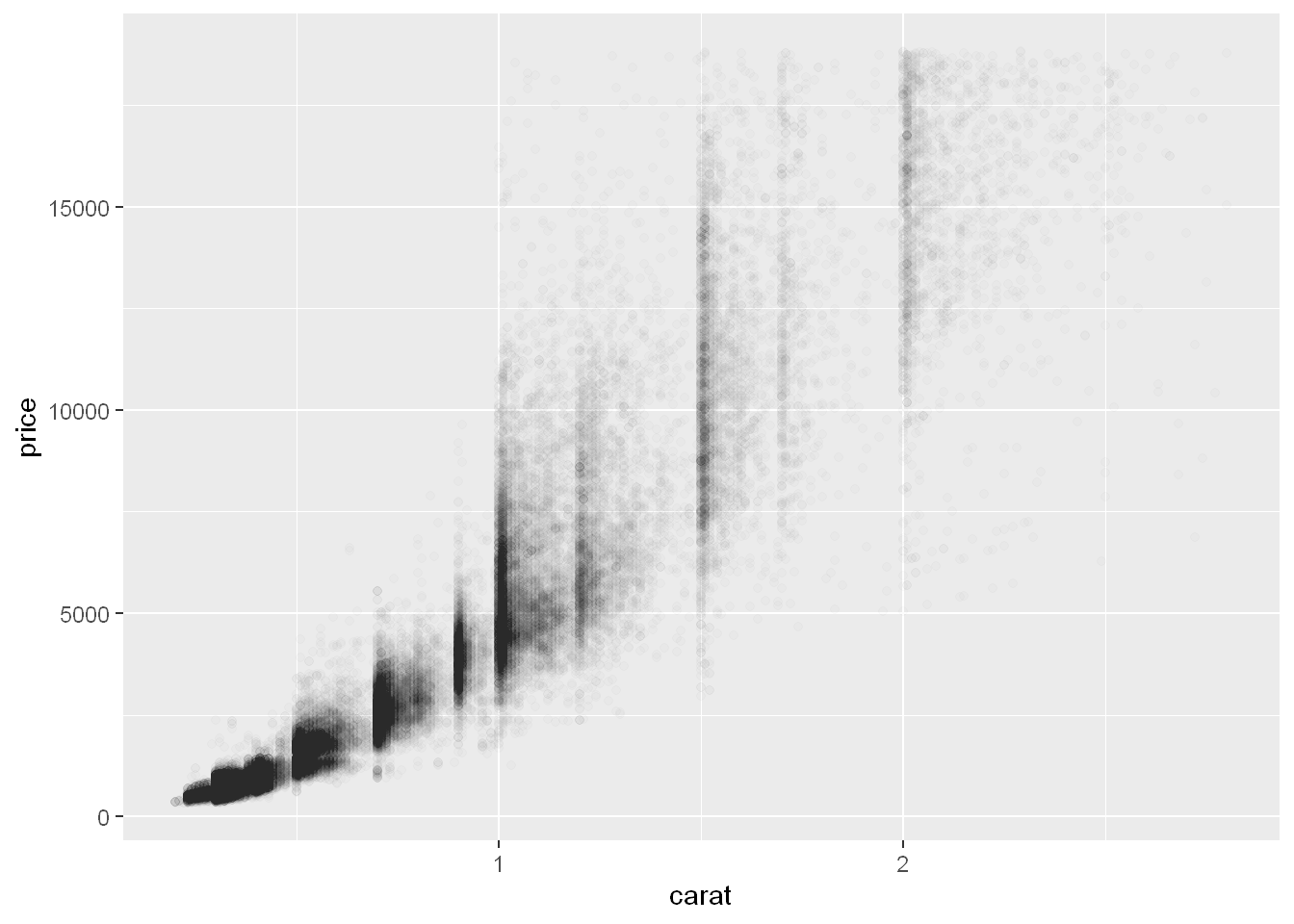

geom_bin2d

geom_hex

But using transparency can be challenging for very large datasets. Another solution is to use bin. Previously you used geom_histogram() and geom_freqpoly() to bin in one dimension. Now you’ll learn how to use geom_bin2d() and geom_hex() to bin in two dimensions.

geom_bin2d() and geom_hex() divide the coordinate plane into 2d bins and then use a fill color to display how many points fall into each bin. geom_bin2d() creates rectangular bins. geom_hex() creates hexagonal bins. You will need to install the hexbin package to use geom_hex().

ggplot(smaller, aes(x = carat, y = price)) +
        geom_bin2d()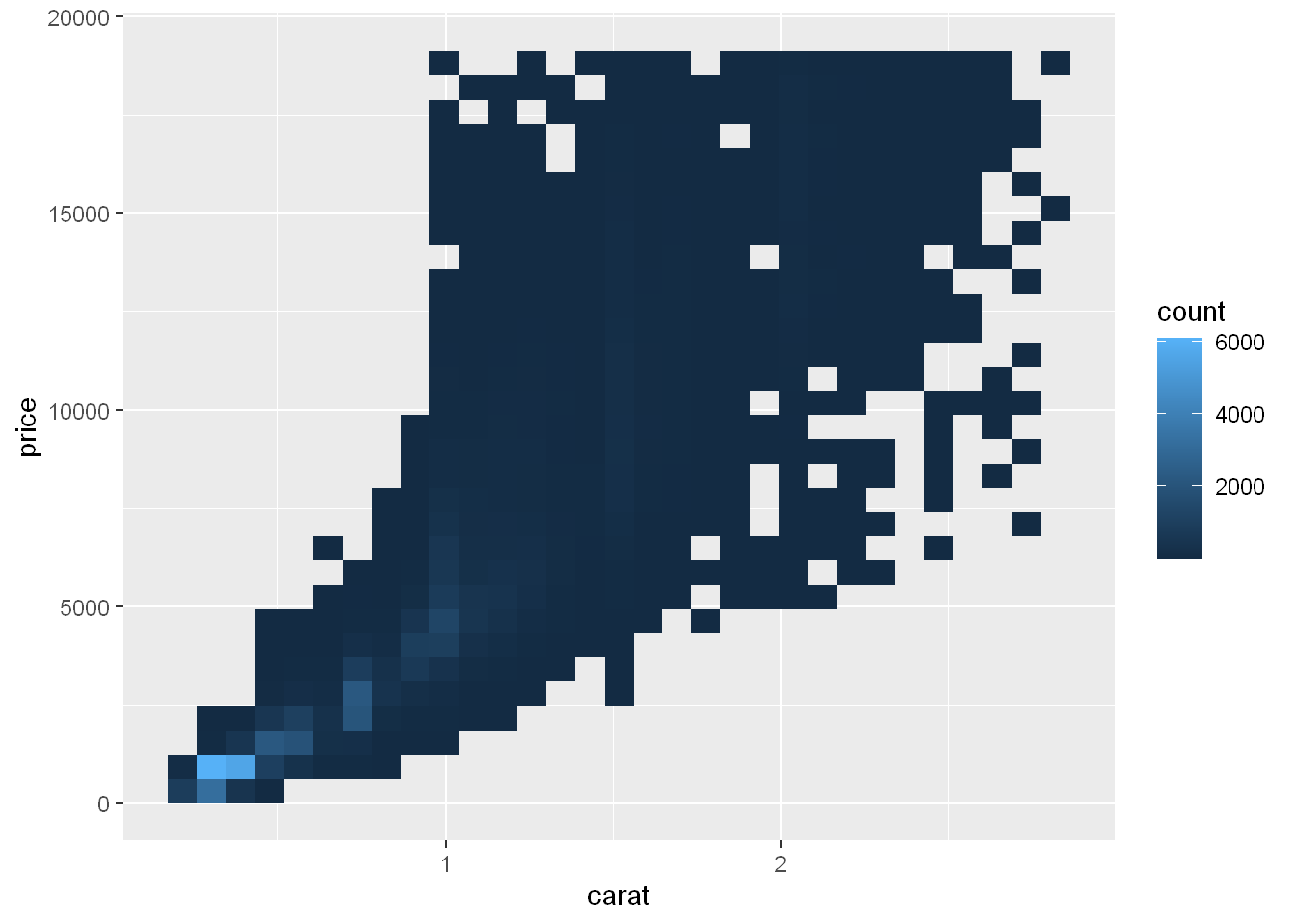 

# install.packages("hexbin")
ggplot(smaller, aes(x = carat, y = price)) + 
        geom_hex()

Warning: Computation failed in `stat_binhex()`.
Caused by error in `compute_group()`:
! The package "hexbin" is required for `stat_bin_hex()`.

Three or More Variables

---

As you’ve guessed by now we can always use aesthetics to map color to one variable while mapping shape to another variable. The plot could become too busy and doesn’t do much to clarify any points we’re trying to convey. Here look at this example, can you tell which shape is which? and by the time you figure that out, you’ll have to learn what each color means.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
        geom_point(aes(color = species, shape = island))

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).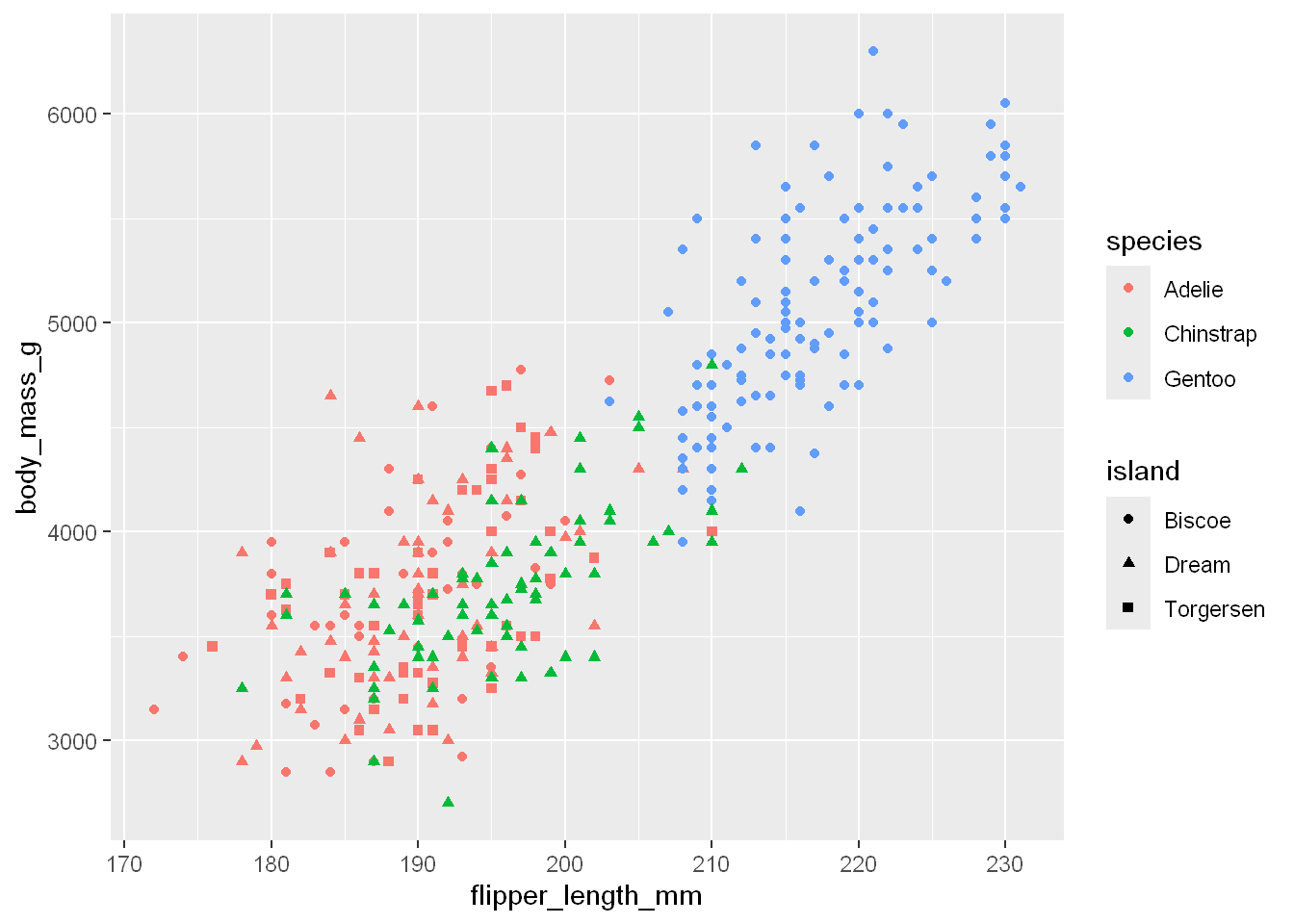

Facets

The better way to do this is by the use of Facets. We already covered it earlier in the page, so I’ll summarize.

facet_wrap

Single variable

To facet your plot by a single variable, use facet_wrap(). The first argument of facet_wrap() is a formula3, which you create with ~ followed by a variable name. The variable that you pass to facet_wrap() should be categorical.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) + 
        geom_point(aes(color = species, shape = species)) + 
        facet_wrap(~island)

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).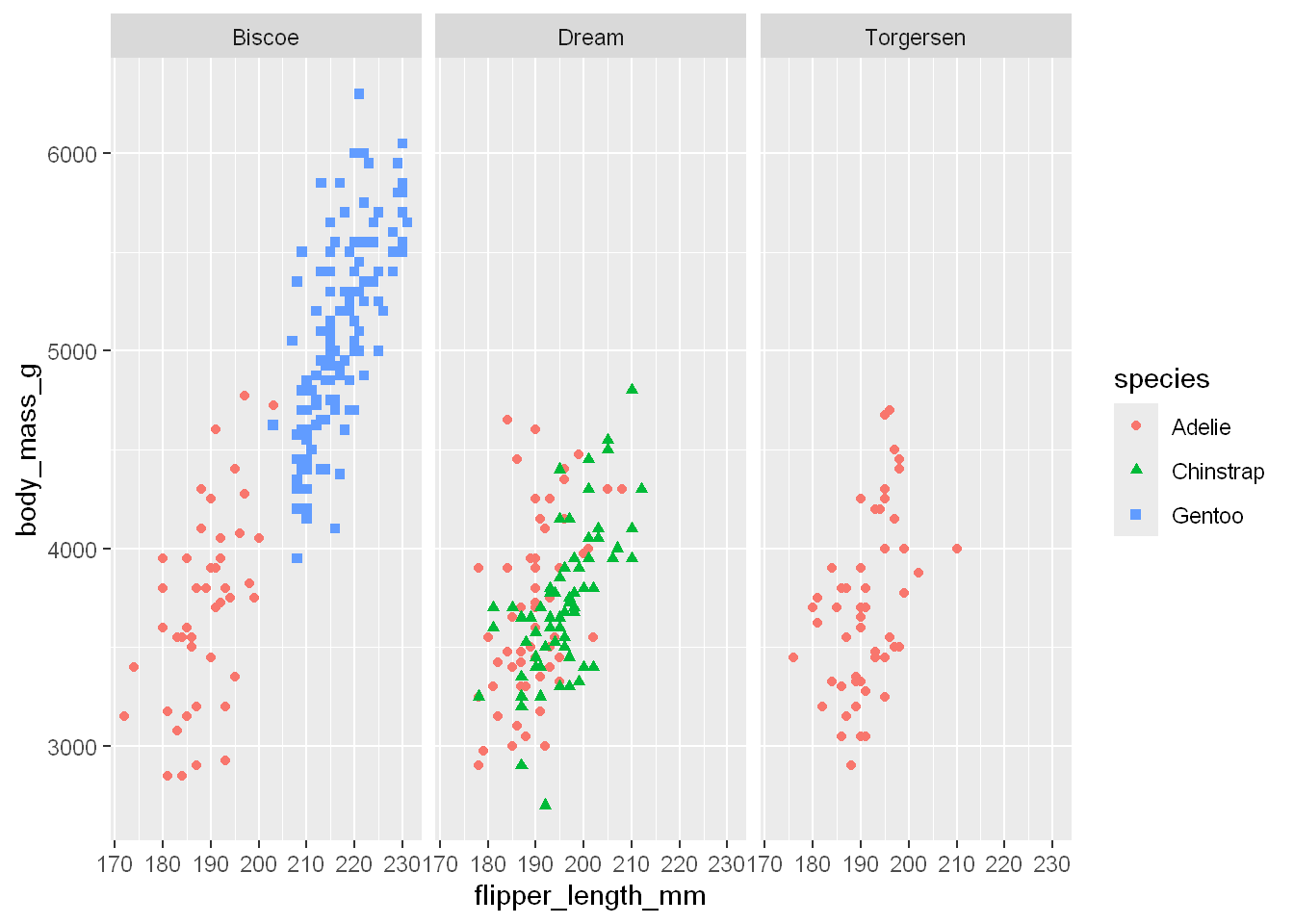

Cut Continuous Variable

---

cut_width

Another option is to bin one continuous variable so it acts like a categorical variable. Then you can use one of the techniques for visualizing the combination of a categorical and a continuous variable that you learned about. For example, you could bin carat and then for each group, display a boxplot:

ggplot(smaller, aes(x = carat, y = price)) + 
  geom_boxplot(aes(group = cut_width(carat, 0.1)))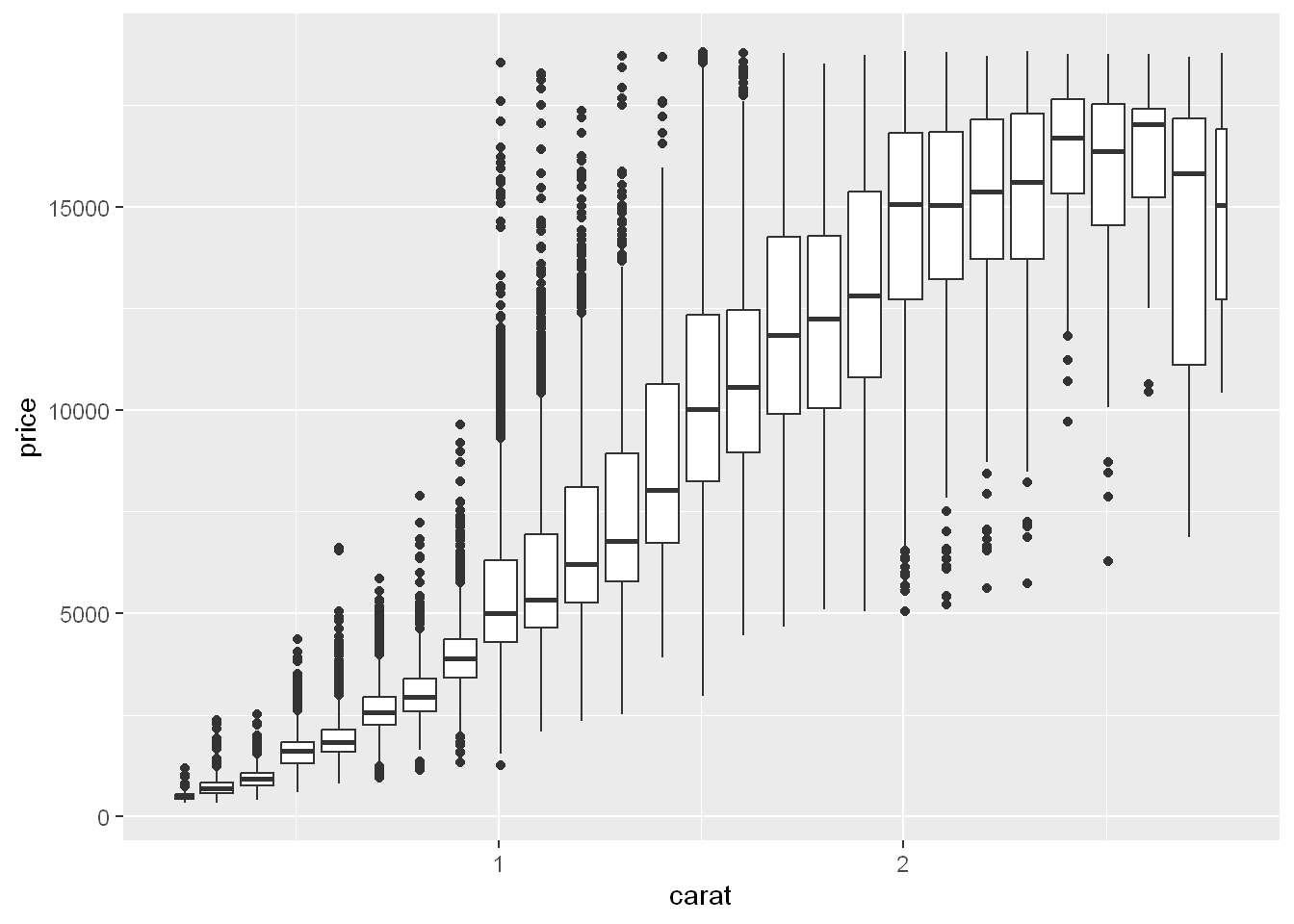

cut_width(x, width), as used above, divides x into bins of width width. Equal width boxes.

By default, boxplots look roughly the same (apart from number of outliers) regardless of how many observations there are, so it’s difficult to tell that each boxplot summaries a different number of points. One way to show that is to make the width of the boxplot proportional to the number of points with varwidth = TRUE.

Observations

1. Instead of summarizing the conditional distribution with a boxplot, you could use a frequency polygon. What do you need to consider when using cut_width() vs. cut_number()? How does that impact a visualization of the 2d distribution of carat and price?

2. Visualize the distribution of carat, partitioned by price.

3. How does the price distribution of very large diamonds compare to small diamonds? Is it as you expect, or does it surprise you?

4. Combine two of the techniques you’ve learned to visualize the combined distribution of cut, carat, and price.

5. Two dimensional plots reveal outliers that are not visible in one dimensional plots. For example, some points in the following plot have an unusual combination of x and y values, which makes the points outliers even though their x and y values appear normal when examined separately. Why is a scatterplot a better display than a binned plot for this case?

coord_cartesian

diamonds |> 
  filter(x >= 4) |> 
  ggplot(aes(x = x, y = y)) +
  geom_point() +
  coord_cartesian(xlim = c(4, 11), ylim = c(4, 11))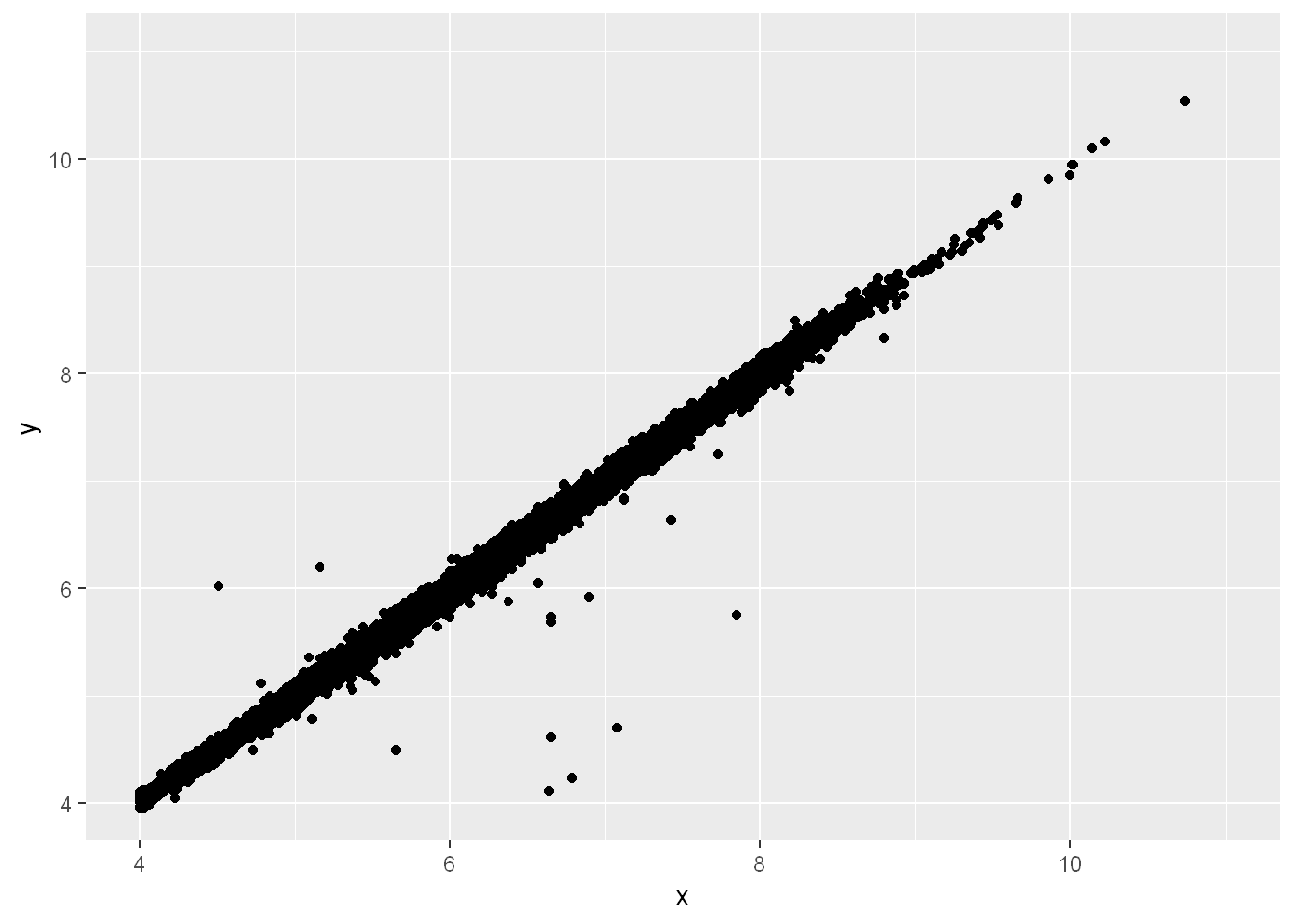

cut_number

Instead of creating boxes of equal width with cut_width(), we could create boxes that contain roughly equal number of points with cut_number().

ggplot(smaller, aes(x = carat, y = price)) + 
  geom_boxplot(aes(group = cut_number(carat, 20)))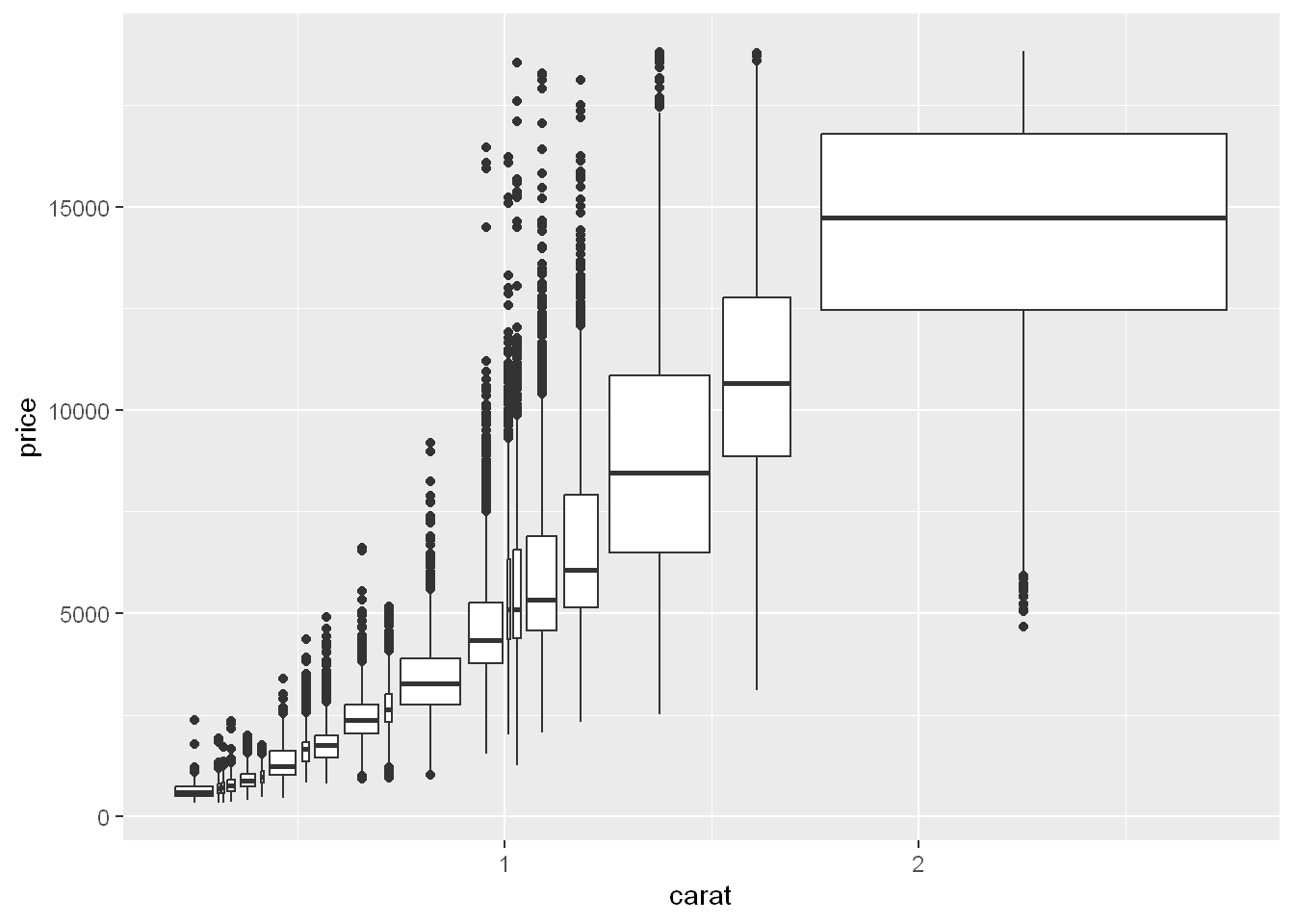

Patterns

---

If a systematic relationship exists between two variables it will appear as a pattern in the data. If you spot a pattern, ask yourself: - Could this pattern be due to coincidence (i.e. random chance)? - How can you describe the relationship implied by the pattern? - How strong is the relationship implied by the pattern? - What other variables might affect the relationship? - Does the relationship change if you look at individual subgroups of the data?

Patterns in your data provide clues about relationships, i.e., they reveal covariation. If you think of variation as a phenomenon that creates uncertainty, covariation is a phenomenon that reduces it. If two variables covary, you can use the values of one variable to make better predictions about the values of the second. If the covariation is due to a causal relationship (a special case), then you can use the value of one variable to control the value of the second.

Models

Models are a tool for extracting patterns out of data.

For example, consider the diamonds data. It’s hard to understand the relationship between cut and price, because cut and carat, and carat and price are tightly related. It’s possible to use a model to remove the very strong relationship between price and carat so we can explore the subtleties that remain. The following code fits a model that predicts price from carat and then computes the residuals (the difference between the predicted value and the actual value). The residuals give us a view of the price of the diamond, once the effect of carat has been removed. Note that instead of using the raw values of price and carat, we log transform them first, and fit a model to the log-transformed values. Then, we exponentiate the residuals to put them back in the scale of raw prices.

library(tidymodels)

diamonds <- diamonds |>
  mutate(
    log_price = log(price),
    log_carat = log(carat)
  )

diamonds_fit <- linear_reg() |>
  fit(log_price ~ log_carat, data = diamonds)

diamonds_aug <- augment(diamonds_fit, new_data = diamonds) |>
  mutate(.resid = exp(.resid))

ggplot(diamonds_aug, aes(x = carat, y = .resid)) + 
  geom_point()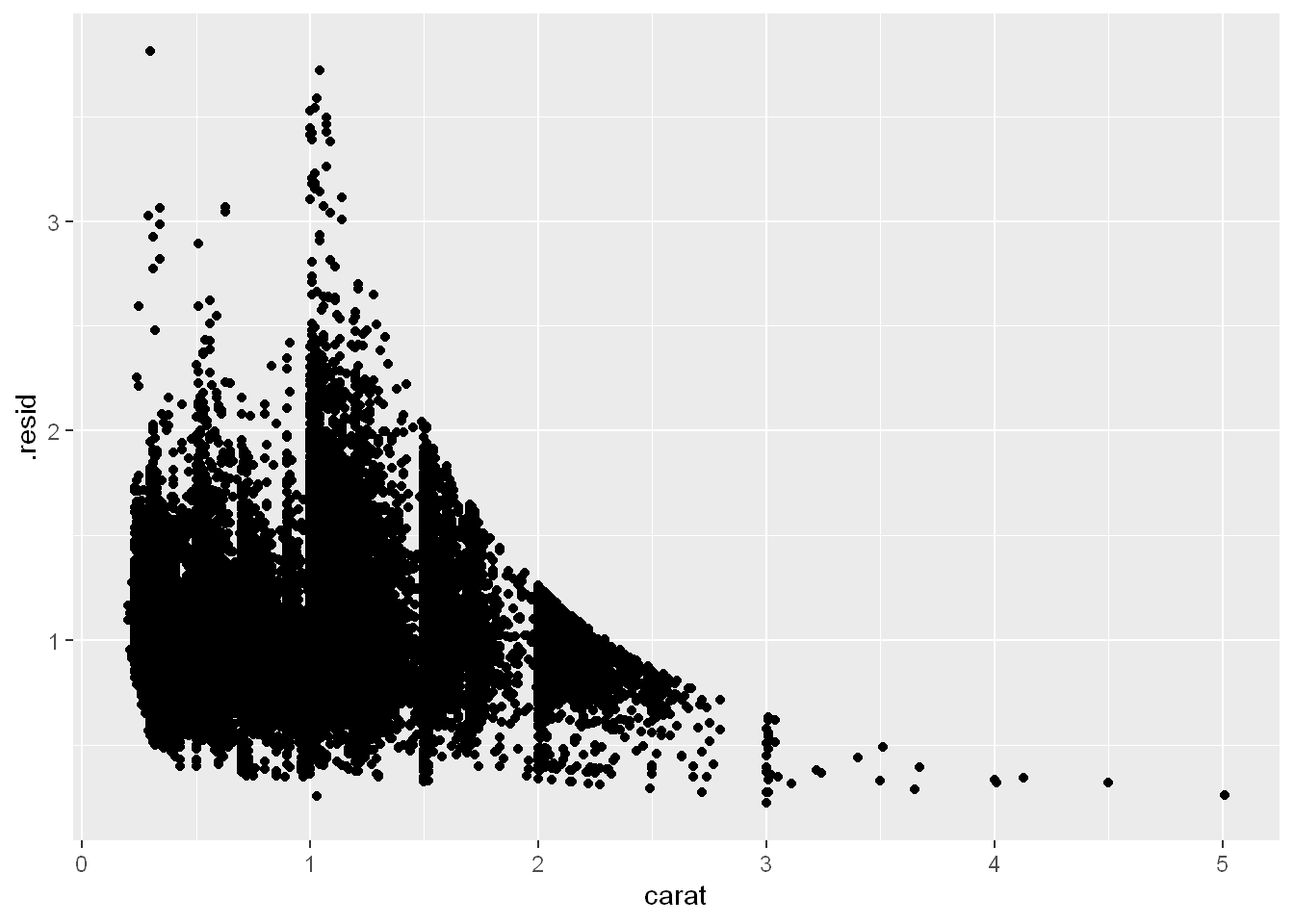

Once you’ve removed the strong relationship between carat and price, you can see what you expect in the relationship between cut and price: relative to their size, better quality diamonds are more expensive.

ggplot(diamonds_aug, aes(x = cut, y = .resid)) + 
  geom_boxplot()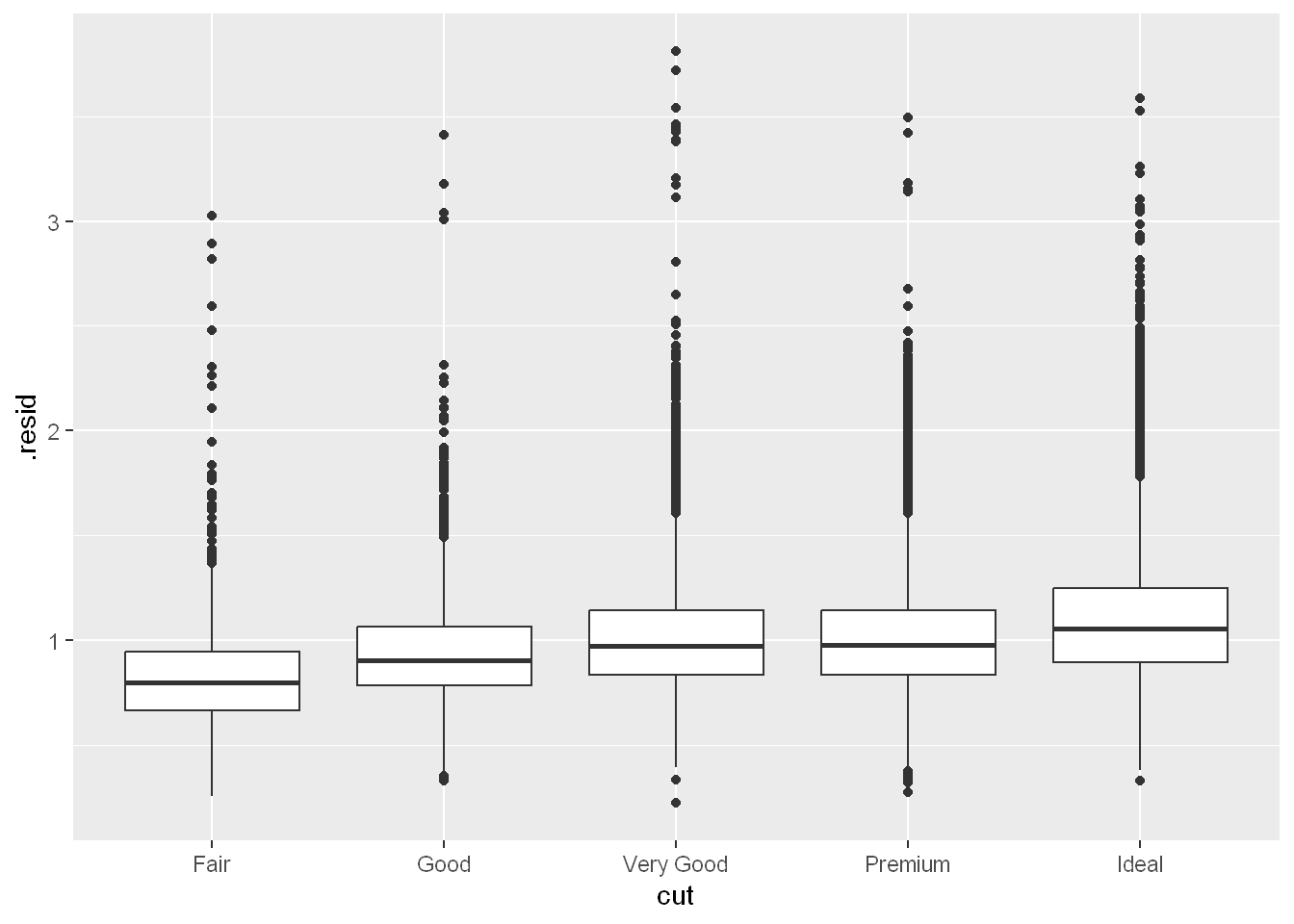

We’re not discussing modelling in this book because understanding what models are and how they work is easiest once you have tools of data wrangling and programming in hand.